Performance of Fibonacci numbers algorithms

Performance of algorithms is important topic if you want to write programs that work fast and doesn’t eat too much resources. In this example I will show you two implementations of famous Fibonacci numbers algorithm and let you compare how these two implementations perform. This posting will be also introduction to my next posting to keep it smaller and to keep focus on point.

You can read more about Fibonacci numbers from Data Structures and Algorithms with Object-Oriented Patterns in C#, chapter Example-Fibonacci Numbers.

Recursive implementation

Our first implementation of Fibonacci numbers uses recursive algorithm. Recursive algorithm is very short and also easy to read.

C# 
public int FibonacciRecursive(int x)
{
    if (x == 0 || x == 1)
        return x;
 
    return FibonacciRecursive(x - 1) + 
           FibonacciRecursive(x - 2);
}

VB.NET

Public Function FibonacciRecursive(ByVal x As Integer) As Integer
    If x = 0 OrElse x = 1 Then
        Return x
    End If
    
    Return FibonacciRecursive(x - 1) + FibonacciRecursive(x - 2)
End Function

Experienced programmers should see here two dangers. First of them gets clear to others at the end of this posting. Second of them is simple: recursive code is harder to debug than flat code.

Flat implementation

The other implementation is not so short but it doesn’t call our algorithm again and again. It is also not so easy to read as first implementation.

C# 
public int Fibonacci(int x)
{
    var previousValue = -1;
    var currentResult = 1;
 
    for (var i = 0; i <= x; ++i)
    {
        var sum = currentResult + previousValue;
        previousValue = currentResult;
        currentResult = sum;
    }
 
    return currentResult;
}
 
VB.NET
Public Function Fibonacci(ByVal x As Integer) As Integer
    Dim previousValue = -1
    Dim currentResult = 1
    
    For i = 0 To x
        Dim sum = currentResult + previousValue
        previousValue = currentResult
        currentResult = sum
    Next
    
    Return currentResult
End Function

Before I say anything else let’s compare performance of those implementations.

Performance

Now let’s see how these implementations perform. I am sure that less experienced programmers will check if these implementations give same results and they will try them with pretty small inputs. But… look at the results.


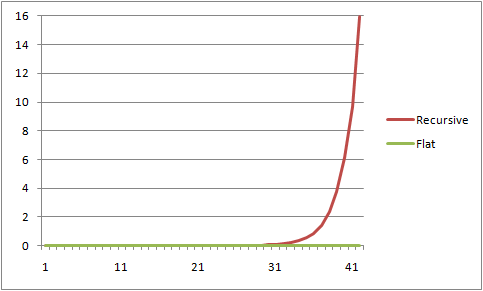
Performance results of recursive and flat implementations of
Fibonacci numbers algorithm.

Horizontal axis shows input integers. Vertical axis shows us time in seconds that calculation took. For smaller inputs both implementations perform very well. Near 30 performance of recursive implementations starts going worse. For the time of last input (that is 41) we are sure that recursive implementation is a highway to hell. But performance of flat implementation is still okay.

This example is good illustration why we must test all the implementations we have before making decision which implementation to use.

Update: Bart Czernicki asked in his comment about F# performance when using recursive calls. I tried it out and F# performs very well in this scenario. In F# you can use recursive calls without any problems as my tests showed me.

kick it on DotNetKicks.com pimp it Shout it

7 Comments

  • Thanks Mark :)
    I suggest my readers to use flat implementations as they perform much better than nested ones.

  • Any discussion on why the flat algorithm performs faster?

  • Hierarchical function calls are less effective because all these calls take memory because of variables used in those functions. Each call waits for two other calls until we receive one of those special cases (0 or 1). And so it goes down in two different branches. If you calculate how much step there are in hierarchies you may be amazed.

    Flat version operates on one set of variables and doesn't make any hierarchical calls. Using only local variables and simple for loop takes less memory and CPU power.

    That's why flat version is faster.

  • Would be interesting if you added an F# recursive implmentation in your test, since it is a functional language optimized for these operations.

  • Thanks Bart, that's the good idea. I will try it out :)

  • Try this. Should be faster than your example versions, though of course, still around 15% slower than F# version that implements the same algorithm.

    public static BigInteger Fibonacci(BigInteger n1, BigInteger n2, int c)
    {
    if (c == 1) return n2;
    Fibonacci2(n2, n1 + n2, c-1);
    }

  • Thanks for good hint, Holystream. I will try your version out for sure.

Comments have been disabled for this content.