Storing Relations revisted - The hanging trees of Pile
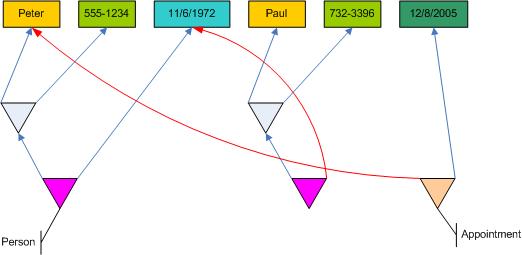
The roots of these trees are at the bottom and the leaves are at the top. Nodes are pointing upwards.
Also I had no answer to the question, how to get to a parent node from its two children. I asked for some function p=f(n,a) (n and a being the left/normative and right/associative children of a node) to "calculate" the parent.
Now, since yesterday I received emails from www.pileworks.org - thanks Miriam! - and have learned, I was on the wrong track. Although my general description is not altogether wrong, it somewhat mixed up things a bit. So let me start to give you an update of my understanding.
First of all I learned to see the tree(s) the right way. They actually start at the top and grow down, it´s hanging trees. Each terminal value truely is the root of an arbitrary number of trees. That also means, children are located below parents. And once we switch views we clearly see, altough each node has only two parents (because it´s a relation connecting two other nodes) it can have any number of children.
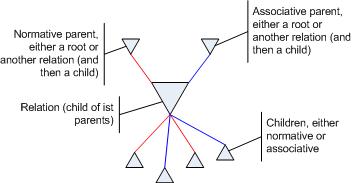
Secondly I realized, all query pattern matching always starts at some root/terminal value. That means, when looking for "te" in the Pile for "Peter" I start out with "t" and "e" and want to find the te-node - which is the only child node belonging to both (!) terminal nodes.
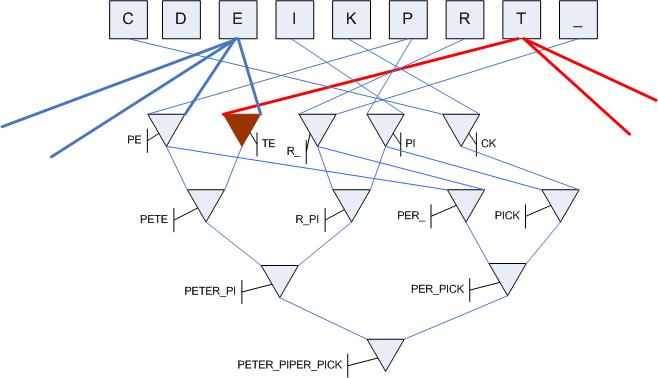
So what looking for ("t", "e") means is: Calculate the intersection of the sets of child nodes of the "t" and the "e" node. The intersection - if not empty - will only contain one node.
After I understood that, I realized my problem of finding f(n,a) vanished. There is no need for such a function. Finding ("t", "e") is just a matter of looking thru lists of child nodes. A simple programming excercise. I then was able to develop a tiny Pile engine within one or two hours which is able to store texts and search for patterns. The core Pile database code is just some 150 lines of code. That was really fun! (However, I´ve to admit I still have some problems searching for patterns. Looking for "Pe" or "te" in "Peter Piper..." works just fine; but looking for "et" does not, because there is no relation between the two; there are only relations ("P", "e") and ("t", "e"), but not ("e", "t"). Hm... But I´m sure the pileworks guys will help me out. I sure still lack some unterstanding of the Pile theory.)
Thirdly I learned from what Miriam wrote and what I saw in a Powerpoint presentation (which I highly recommend to you, if you´re interested in Pile) at www.pileworks.org that Pile distinguishes between two kinds of trees: normative trees and associative trees. The implications of this are not yet clear to me, but I need to adapt my depiction of Piles. If you look at the Powerpoint presentation you´ll see, the pileworks guys have their own diagrams. I kind of find it hard to get used to them. So I try to capture the essence of the two trees in a different way.
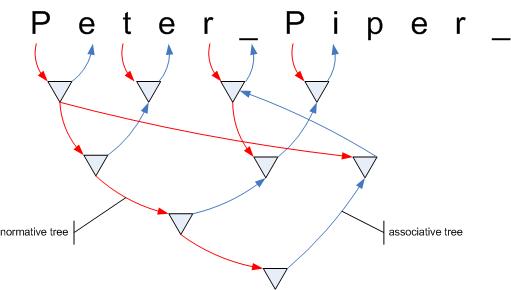
The normative tree is a "real" tree. It starts at a root and spans nodes on lower levels. Build it by following only (!) normative read arrows. The normative tree of "P" for example would be:
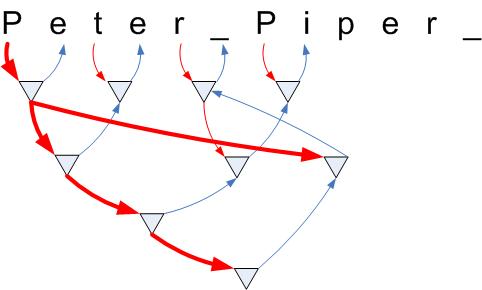
The normative tree for "r" on the other hand would contain "r", r_:("r", "_") and r_Pi:(r_, Pi:("P", "i")).
Associative trees point upwards - although the terminal values are still roots and nodes closer to the top are parents. Here´s the associatve tree for "_" (don´t mind there are no branches in it; that´s due to the simple example):
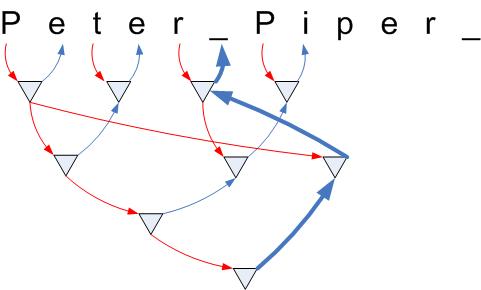
The associative tree is build by only following blue lines; either start from a root node and traverse nodes connected by blue lines - or start at the bottom and follow only blue arrows.
Ah, sigh, I feel relieved now that I clarified this ;-) The pictures now look much more interesting, don´t they? :-)
However, I´m not sure what the distinction between those kinds of trees actually means. Does it help to solve my pattern matching problem? Should I change the data structures in my tiny Pile engine to reflect the changed direction of the arrows? I´ve to ponder this a while... If I find out something, I´ll let you know.