Beyond WinFS - Let associations rule! - or: An introduction to Pile for mere mortals
Yesterday I wrote about why I think WinFS is a step forward - but in the end will not really solve the problem of the penned up data. WinFS´ data units (the objects, e.g. contacts, appointments and what not) simply are still too coarse grained. And even though WinFS puts relations between data units (or entities) more into the center of the stage, it is still bound by the general world view of "data is most important". However, as long as data is in the focus, associations between data are second. And as long as associations are second, we´ll have a hard time to map the multi contextuality of real world entities to software.
Ok, enough said about the limits of current databases technologies. You rightfully ask, how could a different view of the world look like in software. I´ve already written about where I see a promising alternative approach rising above the horizon. See my blog postings on "Storing relations instead of data" and "The hanging trees of Pile". Unfortunately these were early descriptions of something I did not fully understand. Although I´m no "master of Pile" I guess my understanding has evolved and I can now speak with some more confidence, since I´ve implemented a working Pile engine in C#.
So what I´d like to do is provide you with a more systematic introduction to the world of Pile which is all about this new view on handling information. Some two weeks ago I met Erez Elul, the "inventor" of Pile, and Miriam Bedoni his friend who form the main Pile think tank :-) and are constant sources of new insights into the world of associations. They corrected my understanding and deepened it, so I feel confident I can now present the Pile framework for thinking about associative systems in a much clearer way.
Erez (on the left) trying hard to explain some Pile intricacies to my old unenlightened self ;-)
On word of warning, though: I´ll deviate from the terminology and notation Erez and Pile Systems are using and I´ll add stuff, where I think it makes the whole topic more palatable for mere mortals like you and me who have been raised in a data(!)base world. But I hope, once you look at the original documentation about Pile (for example at www.pileworks.org) you´ll find your way around.
Ok, now let´s start our journey thru the Pile universe...
Terminal values and Tops
When I first heard about Pile and "storing data without data" but rather generating data from associations when needed, I asked myself, if that was possible. Where should the data I want to see on my screen come from, if it´s nowhere in the system? It took a moment until I understood, there still needs to be data when working with associations, but it´s just the few data atoms which are needed. Whenever you need the "full data" you assemble it from the data atoms by traversing associations.
Pile calls the data atoms as described in yesterday´s posting Terminal Values (Tv). A Tv is not part of a Pile (that´s how a system of associations is called) or Pile base (as opposed to data base); a Tv is always outside the Pile and a Pile engine (the software managing associations) does not know anything about it. It is ignorant about whether a Tv is a single character or a .jpg-File.
Although the actual data is outside a Pile, there needs to be some way to build associations with it. So there needs to be some representation of Tvs within a Pile. These representations are called Tops.
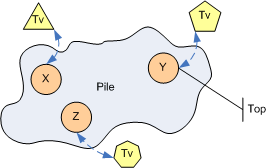
The name Top is supposed to suggest, they are at the very top of the many trees of associations existing in a Pile. Where those trees are I´ll explain in a minute.
Each Tv can only be represented by one Top. And the arrow between Tv and Top in the above picture means: There is a way to get from a particular Tv to its Top and vice versa. But mind you, this mapping between Tv and Top is not part of a Pile or the Pile engine! It´s the responsibility of a so called Pile agent. But more of that later.
The letters in the Top circles stand for some kind of identity. In order to relate "things" they need to be identifiable so each "thing" in Pile has an address, also called handle. More of that later.
Relations aka associations
Pile is not about data, but about relationships. It only knows relationships. Nothing more, nothing less. Pile calls the connection between two "things" relation. However, I prefer the term association, because whenever you talk about relations, people think you talk about relational databases. To abvoid this misunderstanding I´ll often use association instead of relation. But in the end they are interchangeable.
Pile´s relations connect two "things" and are bidirectional.
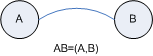
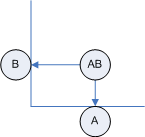
A relation thus can be described by a duple consiting of the left and right "thing": the association between A and B can be written as (A, B). And to give this association a name of its own you can call it AB :-)
Now, what are those "things" that are connected by relations in Pile? Well, those "things" are... relations. Pile only knows relations and thus can only connect relations. That´s part of the beauty of Pile.
A and B are relations as are X, Y, Z in the above picture. Tops are relations too. However, Tops are special in so far as they don´t really connect anything within a Pile. You can think of a Top as an empty relation, e.g. X=(,).
Now comes the twist: Each relation itself again is a relation! The above line between A and B thus is only a logical connection. In reality A and B are connected by a third "entity" called AB:
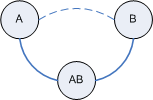
However, in this picture there are again solid lines between relations suggesting new relations. So maybe the most accurate way of depicting Pile relations is like this:
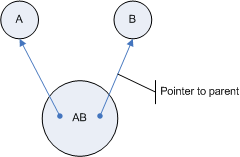
Each relation contains the knowledge of the relations it connects. You could think of this knowledge as pointers to the associated entites. Or you could view it as a containment relationship:
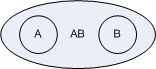
This also makes obvious another property of Pile relations: a relation always only has 2 parents, e.g. A and B for AB.
Howevery, every relation can be parent to an arbitrary number of other relations:
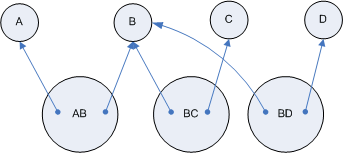
Here relation B is parent to AB, BC and BD.
Tops don´t have parents. They are mapped to their Tv by some other means unknown to Pile. Pile just recognizes Tops as what they are thru the lack of parent pointers.
Defining hierarchies and linking hierarchies
Relations in Pile are not only bidirectional and themselves again parents for new relations, but also directed. Pile relations have a start and an end. The parents play different roles. Or how the Pile theory calls it: relations are related in different manners.
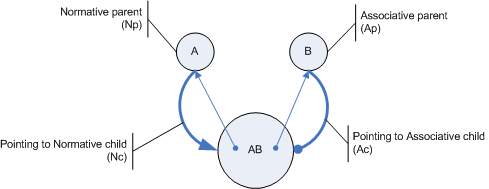
The parent-child relationship between two relations can be in so called normative manner or in associative manner. The Normative parent (Np) of a relation is the origin of it, the Associative parent (Ap) is the destination. So you could read a relation from left to right: A to B or A before B or whatever. (Erez even sees time encoded in Pile relations - but that´s a part I don´t understand yet. He probably alludes to a reading of relations like "A causing B".)
Although the "true pointers" are from a child relation to its two parent relations, the logical connections are from the parents to their children (thick lines in above picture). Each relation can be Np or Ap to an arbitrary number of relations who are then its Normative child (Nc) and Associative child (Ac) relations. And each relation has exactly one Np and one Ap (except for Tops).
It took me quite some time to see why the Pile guys called the manners like this. But in the meantime I guess it´s fair to explain it like this:
- Following the path from parent to child relations along the normative manner defines a hierarchy, a context.
- Following the path from child to parent along the associative manner links relations within a context with other contexts.
When you start at some relation and follow all paths from it to Nc and further down from them to the next level of Nc and so on, you´re traversing a tree. This tree is called the Normative tree and can be thought of as holding together relations with regard to a common concern. We´ll see in a minute, where such trees originate and how they can be used.
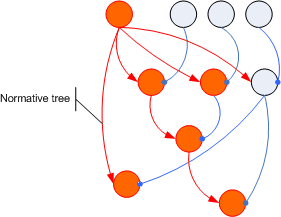
Now when you start at a relation and follow the route of it associative children and the Ac etc. then you get a different tree. It too starts at a single relation, but can also be read from bottom to top. When you follow the direction of the green arrows which means you follow the direction of the child relation which connects Np with Ap, then you´ll find, the associative tree links relations within a normative tree with its top relation.
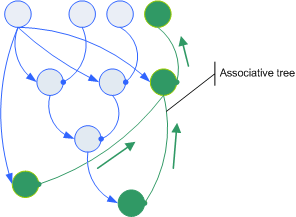
An associative tree can thus can be viewed as a link between or bridge across contexts spanned by different normative trees.
Does that make sense? No, I guess not :-) For you it´s probably just terminology and theory without a relation (sic!) to the real world. But I hope you bear with me, because eventually I hope I can show you how all this can be put to work. Just suspend your disbelief for another moment and try to see it this way: In order to work with new concepts you need words to describe their parts, their structure. Otherwise no communication about the concepts is possible. For the world of RDBMS the terminology is well established. But for the world of associative bases or Pile it is not. That´s why we need to climb up this learning curve first.
Types of relations
Ok, so what do we have? There are Tvs, there are Tops, there are (bidirectional but directed) relations. What can we make of them? We can relate those terms in a systematic way to see patterns. And patterns bring order to chaos, they help to avoid getting overwhelmed by details.
As it turns out, we can classify relations of being one of five types according to the type of their parent relations:
- Top: no parents, representation of a Tv
- (Top, Top): called System Definer (SD)
- (Np, Top): called (Normative) Root (Nr)
- (Top, Ap): called (Associative) Root (Ar)
- (Np, Ap)
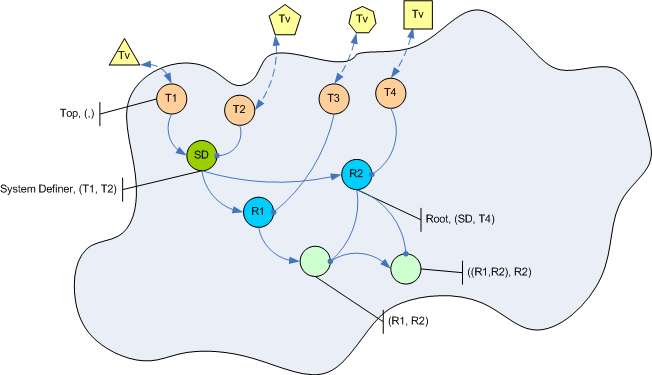
The above picture shows the most important four types of relations. (Top, Ap) I haven´t stumpled across in my work with Pile, so I left it out. I guess, you´ll have no difficulties depicting it yourself.
The SD is somewhat artifical, but nevertheless important. Although its parents are roots, they usually don´t have meaning in the outside world. You can pick some arbitrary Tvs for them. The reason for an SD to exist is not to represent a connection between outside data, but to define a normative tree! Each SD defines a context or (logical) system. It is the origin of a normative tree. Later on we´ll see how this can be used to model a net of associtations for full text search and other applications.
The Root relations then are representations of terminal values within a context. Roots "draw" Tops into the system of a SD. As far as I understand, when you use a Pile to describe data, your associtations never are between Tops or SD and Tops, but always between Roots.
Most relations in a Pile are of the last type: (Np, Ap). None of the parents is a Top. You can think of them as "being somewhere in the middle" of the Pile trees.
Categories for relations
There is one last piece missing in the basic conceptual Pile puzzle: logical categories for relations. In order to be able to distinguish between relations and to "draw circles" around relations somehow belonging to each other, you can assign each relation a so called Qualifier (Q). A relation thus is fully defined as a triple: (Np [Q] Ap).
Alternatively you can think of Q as the color or taste of a relation. It has no meaning to the Pile engine, but needs to be interpreted. A Q without an observer is of no use. A Q thus is assigned and interpreted by a Pile agent.
Uses for Qualifiers can be: categorize all relations describing lines in a text, color all relations according to whether the belong to information or meta-information.
Qualifiers are essential to bound searches within a Pile. They serve as demarkations for certain kinds of information, e.g. when searching for a text pattern you can stop traversal of the associations with Q "text" when hitting a relation of category "line".
When to use Qualifiers and when to use relations to Tops in order to assign some kind of type to a set of relations, I don´t fully understand yet. But my guess is: This is an area where some research needs to be invested.
The Pile space - implementing relations
Ok, now we need to transition from theory to reality. How can implement a Pile? Well, you could say, let each relation be an object with two references to parents and many references to children, e.g.
class Relation
{
Qualifier q;
Relation Np, Ap;
List<Relation> NcList, AcList;
}
Yeah, you could do that. But that wouldn´t let your memory consumption explode. Erez thus suggest to step back and think about a more efficient mapping of relations.
What is a relation? Or let me call it a node or object in a Pile. A node is just a point in a two-dimensional space. It´s coordinates are its parents.
The parent A and B define the point AB=(A,B) in a two-dimensional coordinate system. In so far it seems to suggest itself to represent a relation as a number on an axis in a cartesian coordinate system.
Let A=10, B=15, then AB=(10,15).
And indeed, a relation needs to be nothing more than a unique number - as long as this number somehow encodes the relations it associates with one another.
Now, how about the relation ABC=(AB, C)? With C=22 that would be ((10,15), 22). How to depict that in a 2D-space? Or what about D=25, E=34 and (AB, DE)=((10,15), (25,34))? Where would you locate (10,15) or (25,34) on the x- or y-axis? Not possible, you´re right.
But here comes the rescue:
Assign the point of a relation in 2D-Space a value, a handle...
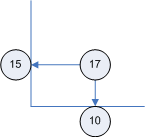
...and use that value as a coordinate, whenever the relation is used as a parent.
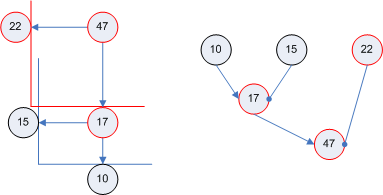
The above picture shows AB (with a handle value of 17) as the Np of another relation (with the handle value of 47).
Since a relation can be normative or associative parent of any number of child relations, it´s handle can serve as x- or y-coordinate for those children. (The x-coordinate represents the normative manner, the y-coordinate represents the associative manner.)
Now, because the same handle value can be used on the x- and y-axis it effectively is a point on the 45° diagonal, where x- and y-coordinates are the same:
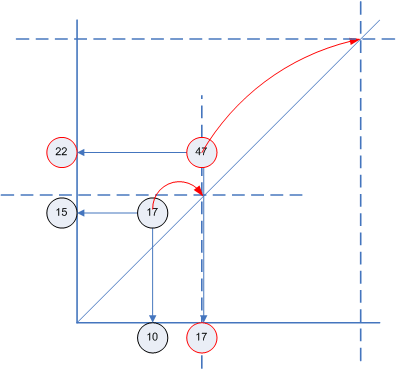
AB=(A,B) is 17=(10,15) and with C=22 leads to ABC=(17,22)=47. Then, when ABC is called to be a parent in another relation, its value 47 is either used as the x-coordinate or the y-coordinate, depending on whether it´s supposed to be the normative or the associative parent.
Pretty ingenious, eh? ;-) By mapping 2 coordinates into 1 Pile avoids a nesting problem as in ((10,15),22) and let´s you represent relations as simple numbers in a 2D cartesian coordinate system. No object orientation needed.
But what about Qualifiers, you might ask. Good question! Qualifiers are encoded in the relation´s handle. The handle value has n bits of which the most significant m < n bits are reserved for Q. Current implementations of Pile engines use 32-bit integers for handles and allocate 8 bits for Q:
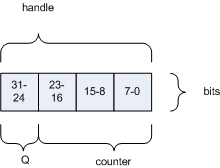
That means, there can be 256 different "colors" for relations and within each Q category some 16 million (2^24-1) relations. Sounds enough for a start, I´d say :-) But if you like, choose the number of bits per handle and for Q as needed.
Since the value of a handle is independent of the values of the handles of the parent relations, a Pile engine can "calculate" it any way it likes. Why then not say: for each Q the value of the remaining bits (24 in the above example) is viewed as a counter. For each new relation with a particular Q the Q´s handle counter is incremented, packed to gether with the Q value and returned as the handle for the relation.
Here´s how I do this in my C# Pile engine:
private int[] qualifierCounters = new int[256];
public int CreateHandle(byte qualifier)
{
return ((int)qualifier) << 24 | ++qualifierCounters[qualifier];
}
With handles and a coordinate system in hand, we now can think about how to integrate all this into one homogeneous picture. How can we map the different types of relations into the the 2D Pile space? Here´s Erez doing it for us (with some attendees of the recent Pile workshop in Berlin).
It really took me a while before I understood what he was drawing... but in the end I think it´s so simple and straightforward as to signify something important. His Pile space looks like this:
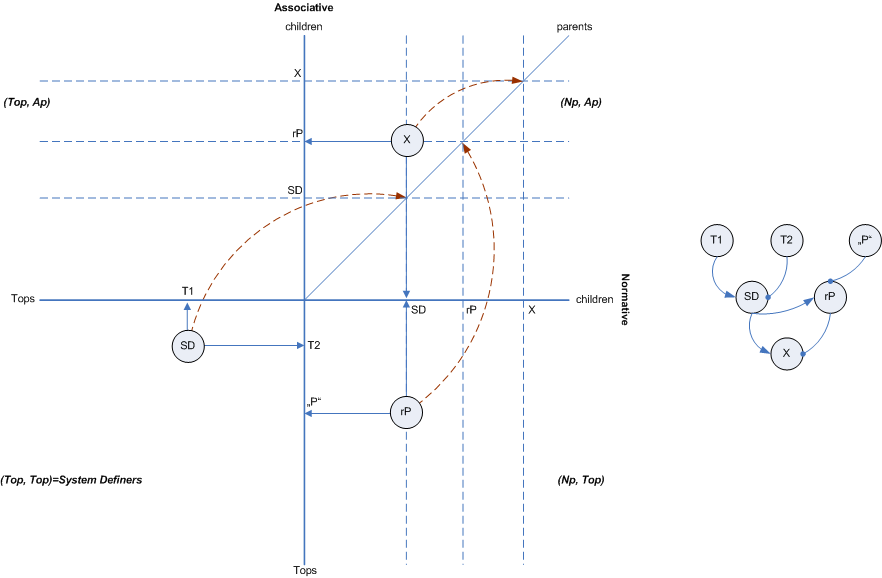
So far I´ve shown only the top right quadrant of the coordinate system. But in fact it´s made up by all 4 quadrants, each for one of the non-Top types of relations.
The negative parts of the axises are reserved for Top relations. They don´t have parents. So when you combine two Tops to form a System Definer relation you get a point in the lower left quadrant, e.g. SD=(T1, T2). T1 is the Np, so it´s located on the x-axis, T2 is the Ap, so you find it on the y-axis. This quadrant usually only contains very few relations.
The point SD, as explained above, gets assigned it´s own handle, SD, which is a positive value and defines a point on the parent diagonal in the upper right quadrant. This point necessarily lies on this diagonal, because it can be used as the x- or y-parent coordinate of another relation depending on whether SD is the Np or Ap.
Take the relation between Top for Tv "P" and the SD for example. rP=(SD, "P") is a normative root since its Np is not a Top, but its Ap is. To locate the rP relation in the 2D space the value of its Np is used as the x-coordinate and the value of its Ap is taken as the y-coordinate. Then rP is assigned a value of its own which locates it on the parent diagonal.
Normative roots are located in the lower right quadrant. Ar are located in the upper right quadrant.
Now if you want to relate the SD with rP to and creat relation X, you use SDs handle as the x-coordinate and the rP handle as the y-coordinate since X=(SD,rP). Then X is assigned a value of its own. This type of relation - (Np,Ap) - is the most common one. So the top right quadrant will be pretty densely populated.
And all the handles of all relations lie on the parent diagonal! Or to say it differently: All relations are located on a single line starting at (0,0) and ending at (2^32-1,2^32-1). Or even simpler: all relations are in the range of 0 to 2^32-1.
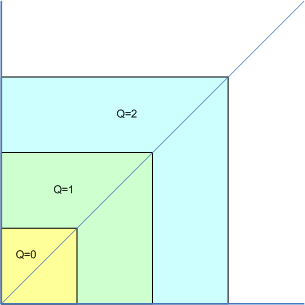
But the distribution of handles on this line is not equal. The line (or diagonal) is segmented by Q!
What we now have is a mapping of A and B to AB. We can move through a Pile from the Tops down... We can easily get from two parents to the child relation connecting them.
But when traversing networks of associtations we surely also want to go in the other direction. So we need a way to locate the Np and Ap of a given relation.
This is done by introducing a z-axis into the picture. Each handle value is also located on the z-axis and its "point" there does not contain a handle, but it x-/y-coordinates: With r=(x,y) there is (x,y)=z(r).
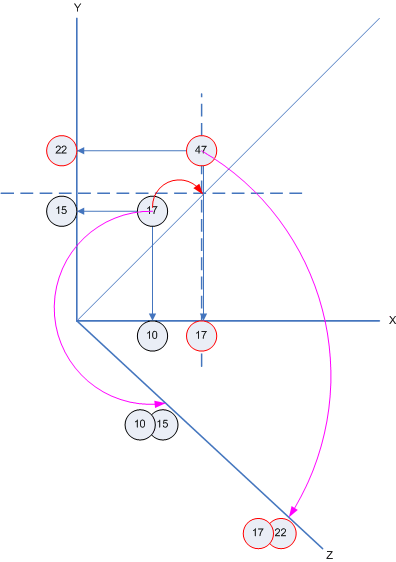
So if you got a relation in your hands, take the handle and go to the z-axis. Lookup the value for this child handle: it´s a pair of handles, the x- and y-parent-coordinates of the child handle. Whereas a point in the 2D coordinate system hold 1 handle value, a point on the z-axis contains 2 handle values. Once I show you some code, you´ll see it´s very easy.
Pausing for a moment
That´s pretty much it. More you don´t need to implement you first Pile engine. Let´s pause for a moment.
Sure, there are lot´s of open questions and many things to research. But the general concept of an AB, an associative base, or a Pile as Pile System calls it, are layed out. The world of associations and even their most basic representation has been defined. No more data to be seen. It´s all outside the system. Inside are just relations and relations between relations.
Stop thinking in data, start thinking in associations or relations.
What´s next? Next I´ll show you my small Pile engine and talk about Pile agents. Stay tuned!

