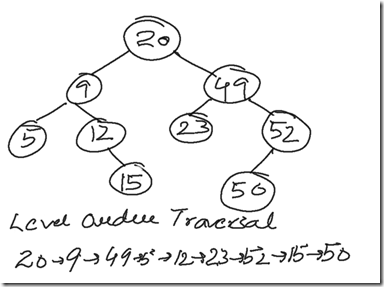
In a binary tree, node level is defined as the number of nodes which are in between the node in context & the root node. If we consider root node is at level 0, then immediate child nodes of root are at level 1 and the subsequent child nodes are level 2 and so on. Thus level order traversal of a binary tre involves processing nodes on the basis of their levels i.e. level 0 nodes are to be processed before nodes at level 1 which are to be processed before nodes which are at level 2 etc. The screenshot below shows a tree and its corresponding level order traversal :

Implementation

• We need a class/struct for representing node in the binary tree.
• Traversal logic : As described above, level 0 has to be processed before level1 and level1 before level2. This sounds like queue(FIFO). In our implementation, we will be making use of Queue data structure, to keep the described ordering in place. Steps :
  • Push the root node in a queue
  • Loop till queue is not empty :
    • Pop out an item(i1) from queue & print it
    • If i1.Left != null, then enqueue i1.Left
    • If i1.Right != null, then enqueue i1.Right

Code

void Main()
{
    Node n20 = new Node(20);
    n20.Left = new Node(9);
    n20.Left.Left = new Node(5);
    n20.Left.Right = new Node(12);
    n20.Left.Right.Right = new Node(15);
    n20.Right = new Node(49);
    n20.Right.Left = new Node(23);
    n20.Right.Right = new Node(52);
    n20.Right.Right.Left = new Node(50);
    
    LevelOrderTraversal(n20);
}

public class Node
{
    public Node Left {get; set;}
    public Node Right {get; set;}
    public bool IsVisited {get; set;}
    public int Value {get;set;}
    
    public Node(int value)
    {
        this.Value = value;
    }
}

public static void LevelOrderTraversal(Node node)
{
    if(node == null) return;
    Queue<Node> queue = new Queue<Node>();
    queue.Enqueue(node);
    
    while(queue.Count != 0)
    {
        Node item = queue.Peek();
        
        if(item.Left != null)
            queue.Enqueue(item.Left);
            
        if(item.Right != null)
            queue.Enqueue(item.Right);
            
        Console.Write(item.Value + " -- ");
        queue.Dequeue();
    }
}