In this blog post, I am going to talk about the Key Indexed Counting Sort algorithm. Unlike other generalized sorting algorithms like quicksort, merge sort etc. key indexed counting sort algorithm is a specialized sorting algorithm which works best when the following conditions are met:

• Input consists of collection of n items
• Maximum possible value of each of the individual item is K

For e.g. consider the following string : “abcddcabbcddaa”. As we can see the string is made up of following four characters : { ‘a’, ‘b’, ‘c’, ‘d’ }. Thus we can make use of counting sort to sort the string based on the individual character values. Other possible use cases of counting sort includes:

• Sort collection of integers where the numbers are in the range 1-N
• Counting sort plays crucial roles in other advanced algorithms like LSD & MSD string sort
• Sorting DNA string

Lets move on the implementation of Counting Sort algorithm and see how it can be used to sort the previously defined string.

Steps

• Identify the domain of possible input values e.g. in the above mentioned string possible values of individual characters are { ‘a’, ‘b’, ‘c’, ‘d’ }. If the domain values are not known in advance, then it can be easily determined by making a single pass over the input collection & determining the unique input values.
• Declare an auxiliary array of size equal to that of input collection. It’s needed to store then intermediate sorted collection.
• Another array of size equal to the number of domain values + 1. Initialize this array with domain values starting with position 0.
• Implementing counting sort using the above mentioned data structure involves
• Run through the input collection and for every element, search it in domain values array and increment its corresponding count
• Next, run through the domain array and for every cell, increment its value by adding to it the value of its previous cell
• Again run through the input collection, for every element get the index count value from domain array and insert that value in auxiliary array at that index. Once inserted, increment the index value of the corresponding domain array.
• Finally copy the values back from auxiliary array to the main array.

I will depict the steps mentioned above with diagrams by trying to sort the “abcddcabbcddaa” using counting sort. Let’s see the full implementation of counting sort along with helpful diagrams.

void Main()
{
    char[] items = new char[] {'a', 'b', 'c', 'd'};
    KeyIndexedCountingSort sort = new KeyIndexedCountingSort(items);
    var result = sort.Sort("abcddcabbcddaa");
}

public class KeyIndexedCountingSort
{    
    private List<char> _charSet;
    public KeyIndexedCountingSort(char[] charSet)
    {
        _charSet = charSet.ToList();    
    }
    
    public char[] Sort(string data)
    {
        char[] auxArray = new char[data.Length];
        int[] keyIndex = new int[_charSet.Count() + 1];
        
        for(int i = 0; i < data.Length; i++)
        {
            keyIndex[_charSet.IndexOf(data[i]) + 1] += 1;
        }
        
        for(int i = 1; i < keyIndex.Length; i++)
        {
            keyIndex[i] += keyIndex[i - 1];
        }
        
        for(int i = 0; i < data.Length; i++)
        {
            var index = keyIndex[_charSet.IndexOf(data[i])];
            auxArray[index] = data[i];
            keyIndex[_charSet.IndexOf(data[i])]++;
        }
        
        return auxArray;
    }
}

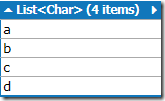
Lets see what the _charSet collection looks like:

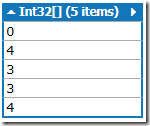
Now lets see what the keyIndex array looks like after the end of first for loop. Note : we are adding items to the keyIndex array by get index of char from _charSet collection & then adding 1 to it.

for(int i = 0; i < data.Length; i++)
{
    keyIndex[_charSet.IndexOf(data[i]) + 1] += 1;
}

Once the keyIndex array is initialized, then let see its state after the end of second for loop:

for(int i = 1; i < keyIndex.Length; i++)
{
    keyIndex[i] += keyIndex[i - 1];
}

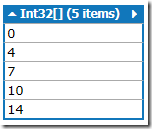
From the above pic, its clear that a cell value is incremented by adding current value with that of previous cell value. Finally lets see the counting array in action i.e. how content of input array is mapped in sorted order into auxiliary array using intermediate keyIndex array.

for(int i = 0; i < data.Length; i++)
{
    var index = keyIndex[_charSet.IndexOf(data[i])];
    auxArray[index] = data[i];
    keyIndex[_charSet.IndexOf(data[i])]++;
}

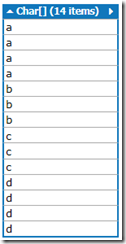
As we can see the data is sorted. Next we can copy the content from auxiliary array back to input array. In the next blog post, we will see how counting sort is used for implementing LSD string sort algorithm.