Secrets of the Grey Beards: drawing circles with additions and shifts
A long time ago, before GPUs, before multicore processors and gigabytes of RAM, clever algorithms were the only way to render complex graphics in real-time. Those algorithms are now mostly forgotten as nobody needs them or is interested in them. Nobody? Well, almost. I like to reverse-engineer the clever tricks programmers of that era were using (in fact, I was one of them), and I hope you'll follow me on this exploration.
In this post, I'm going to show you algorithms that solve the seemingly simple task of drawing a circle, and we'll do so with very strong constraints on the operations we're allowed to use. In the early days of video games, the late 70s and early 80s, the processors in home computers and game consoles were mostly 8-bit processors such as the 6502 and the Z80. Those processors were not only slow by today's standards with frequencies around 1-2MHz and no parallel execution of any kind, they had very limited instruction sets, without multiplication and division operations, and with only support for integer numbers. That doesn't mean that multiplications were impossible, but just that they were very, very expensive. As a consequence, algorithms avoiding them were preferable.
Operations that 8-bit processors were very good at running fast, because they can be implemented with few simple logic gates, include additions and bit shifting.
The way mathematicians would describe circles is often with equations such as or .
Both of those involve multiplications, or worse, trigonometric function evaluation. So what are we to do?
The first thing we can notice is that the first equation is quadratic, so everything in there, once differentiated, becomes linear, and as such, easy to compute using additions and multiplications by constants. Let's keep that differentiation idea but it's the second system of equations that I'm going to differentiate, to come up with the first algorithm:
We can then notice that we can spot the expressions for and in those differential equations and reformulate them as follows.
What that tells us is that when the angle changes by an infinitesimally small amount , changes by and changes by . This still contains a multiplication, but only by the constant amount we want to vary the angle between two steps of the rendering. If we choose that amount to be the inverse of a power of two so that the corresponding change in coordinate is always under one pixel, thus ensuring continuity, we can avoid the multiplication because multiplication by the inverse of a power of two is the same as shifting bits to the right by a number of bits that is that power: x/2^n is the same as x >> n.
We still have the problem of determining the value of , but we only have to do it once per circle, so this is less of a hot path. It turns out, all you have to do is shift 1 left (which is the same as enumerating powers of two) until you run over :
| let n = 0; | |
| for (let twopown = 1; twopown < r; n++, twopown <<= 1); |
And this is it, we now have a working algorithm:
| // Now we can start from (r, 0) and apply the differential equations at each step | |
| let x = r << bdp, y = 0, t = 0; | |
| while (x >= y) { // We only need draw 1/8th of the circle, symmetries will do the rest | |
| const [screenx, screeny] = [x >> bdp, y >> bdp]; | |
| drawPointAndSymmetries(ctx, xc, screenx, yc, screeny); | |
| // Side effect: it's trivial to derive a table of sine and cosine values | |
| // from this algorithm while we're here... | |
| sine[t] = y; | |
| cosine[t] = x; | |
| t++; | |
| // Apply the differential equations | |
| [x, y] = [x - (y >> n), y + (x >> n)]; | |
| } |
The call to drawPointAndSymmetries is just using the axial symmetries of a circle to only compute one eights of the circle:
| function drawPointAndSymmetries(ctx, xc, screenx, yc, screeny) { | |
| // Draw the current pixel and all its easily computable symmetries | |
| ctx.fillRect(xc + screenx, yc + screeny, 1, 1); | |
| ctx.fillRect(xc - screenx, yc + screeny, 1, 1); | |
| ctx.fillRect(xc + screenx, yc - screeny, 1, 1); | |
| ctx.fillRect(xc - screenx, yc - screeny, 1, 1); | |
| ctx.fillRect(xc + screeny, yc + screenx, 1, 1); | |
| ctx.fillRect(xc - screeny, yc + screenx, 1, 1); | |
| ctx.fillRect(xc + screeny, yc - screenx, 1, 1); | |
| ctx.fillRect(xc - screeny, yc - screenx, 1, 1); | |
| } |
If you're wondering about bdp, this is the fixed point bit depth that we use to make decimal calculations using only integers. It's 8 in the sample below, meaning eight bits of precision under the decimal point.
This works fine, but we can do better and faster.
Imagine we wanted to walk the circle in the dark. If we could erect a wall around the circle, we could just walk straight ahead and whenever we hit the wall, take a lateral step away from it. This strategy produces a trajectory that is very close to the circle. It also works on any concave shape, not just circles.
The wall in question is called a discriminating function. It's a function of the coordinates that evaluates as positive outside of the shape and as negative inside. It's called discriminating because by just evaluating it on a point, you can discriminate whether you are inside or outside.
For a circle, it's easy to build a discriminating function from the circle's equation: .
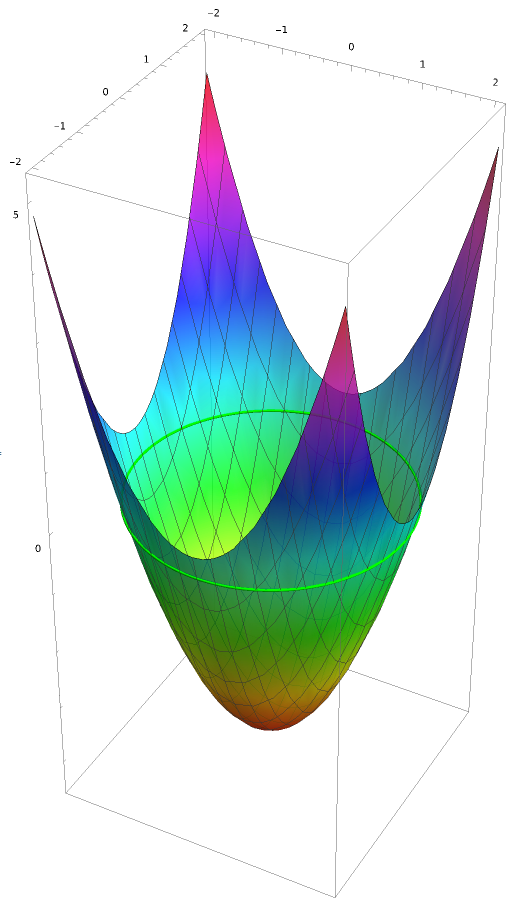
It may seem like computing this function for every point is going to be challenging because of all those squarings. In this case again, variations of the function from pixel to pixel are going to be sufficient if we know the value at any point.
When we move one pixel to the right, here's how the function varies:
This is of course very easy to compute: shift left and add one.
Whenever the new value of the discriminating function goes positive, we need to make a side step, for which it is also easy to compute the discriminating function variation:
Subtract left-shifted from one.
You may also notice that this second algorithm has no need for fixed-point decimal numbers, it can work on regular integer coordinates, which further simplifies it and makes it more efficeint.
Here's the implementation:
| // Start with a value half a pixel inside the circle: f(0, r - 1/2) = 1/4 - r and 1/4 falls below precision. | |
| let x = 0, y = r, f = -r; | |
| drawPointAndSymmetries(ctx, xc, x, yc, y); | |
| while (x <= y) { // We only need draw 1/8th of the circle, symmetries will do the rest | |
| // Draw the current pixel and all its easily computable symmetries | |
| f += 1 + x << 1; | |
| x++; | |
| drawPointAndSymmetries(ctx, xc, x, yc, y); | |
| if (f > 0) { | |
| f += 1 - y << 1; | |
| y--; | |
| drawPointAndSymmetries(ctx, xc, x, yc, y); | |
| } | |
| } |
You can see both of those algorithms in action below:
The source code can be found here: https://github.com/bleroy/3d-junkyard/tree/main/AddAndShift
But of course, this is javascript running on a modern computer, and I sold this as a way to draw a circle on vintage 8-bit computers. Does it work on old computers? Yes, of course it does. Here's the algorithm implemented and running on an Atari 8-bit computer in 6502 assembly (what you see below is an actual emulator in your browser, hosted by the excellent https://8bitworkshop.com; if you see the circle as a little oval, that's normal, vintage computers often have pixels that are not exactly square):
Here's the source code for this:
| ; Atari 8-bit "Draw circle" sample code | |
| ; Written by Bertrand Le Roy | |
| ; Assemble with DASM | |
| ; This draws a 100px diameter circle on the screen in 160x100 resolution | |
| processor 6502 | |
| include "atari.inc" | |
| ;Local constants | |
| R = 50 ;Circle radius | |
| CY = 50 ;Y coordinate of the screen center | |
| LINE_ADDRESSES_MSB = $1200 ;Table of most significant bytes of addresses of the center of each scan line | |
| LINE_ADDRESSES_LSB = $1280 ;Table of least significant bytes of addresses of the center of each scan line | |
| PLOT_VECTOR = $D0 ;Vector used to plot pixels | |
| CURRENT_COL_OFFSET = $12FF ;Used to store the current byte offset for the column to plot | |
| CURRENT_BIT_MASK = $12FE ;Used to store the mask to turn on the current pixel | |
| CURRENT_REV_MASK = $12FD ;Used to store the mask to turn on the current symmetric pixel | |
| X = $12FC ;Stores the x coordinate of the current circle pixel | |
| Y = $12FB ;Stores the y coordinate of the current circle pixel | |
| F = $12FA ;Stores the current value of the discriminating function | |
| org $a000 ;Start of left cartridge area | |
| Start | |
| ;Setup colors, display width and display list location | |
| lda #$28 | |
| sta COLOR0+0 | |
| lda #$00 | |
| sta COLOR0+1 | |
| lda #$06 | |
| sta COLOR0+2 | |
| lda #$58 | |
| sta COLOR0+3 | |
| lda #$D4 | |
| sta COLOR0+4 ; bakground | |
| lda #$00 ;Set Display list pointer | |
| sta SDLSTL ;Shadow DLISTL | |
| lda #$A2 | |
| sta SDLSTH ;Shadow DLISTH | |
| lda #$22 | |
| sta SDMCTL ;Shadow DMACTL (playfield width) | |
| cld | |
| generatelineaddresses | |
| ;Pre-compute addresses for the middle of each line | |
| lda #$20 ;Start from $200A | |
| sta LINE_ADDRESSES_MSB ;Store the most significant bytes to $1200... | |
| lda #$0A | |
| sta LINE_ADDRESSES_LSB ;And least significant bytes to $1280... | |
| ldx #0 | |
| nextline | |
| clc | |
| lda LINE_ADDRESSES_LSB,x | |
| adc #20 ;Add 20 for each scan line | |
| sta LINE_ADDRESSES_LSB + 1,x | |
| lda LINE_ADDRESSES_MSB,x | |
| adc #0 | |
| sta LINE_ADDRESSES_MSB + 1,x | |
| inx | |
| cpx #100 ;Stop at line 100 | |
| bne nextline | |
| plot_circle | |
| ;Plot the circle | |
| ;Initialize x,y and initial value of f | |
| lda #0 | |
| sta X | |
| lda #R | |
| sta Y | |
| eor #$FF | |
| adc #$01 | |
| sta F ;F=-R initial value | |
| jsr plot_symmetries | |
| circle_loop | |
| ;f+=1+x<<1;x++ | |
| ldx X | |
| txa | |
| inx | |
| stx X | |
| asl | |
| clc | |
| adc #1 | |
| clc | |
| adc F | |
| sta F | |
| jsr plot_symmetries | |
| lda F | |
| bmi skip_lateral | |
| beq skip_lateral | |
| ;f+=1-y<<1;y-- | |
| ldy Y | |
| tya | |
| dey | |
| sty Y | |
| asl | |
| eor #$FF | |
| clc | |
| adc #2 | |
| clc | |
| adc F | |
| sta F | |
| jsr plot_symmetries | |
| skip_lateral | |
| sec | |
| lda X | |
| cmp Y | |
| bmi circle_loop | |
| ;We're done. Do nothing for a while. | |
| wait | |
| nop | |
| jmp wait | |
| plot ;Plots the pixel at x+80,y and 80-x,y | |
| txa ;x has the x coordinate | |
| lsr ;5 most significant bits are the offset | |
| lsr ;of the byte where the pixel is | |
| lsr | |
| sta CURRENT_COL_OFFSET | |
| txa | |
| and #$07 ;3 least significant bits point to the bit for the pixel | |
| tax | |
| lda pixelmasks,x | |
| sta CURRENT_BIT_MASK ;CURRENT_BIT_MASK now has the bit mask for the new pixel | |
| lda reverse_pixelmasks,x | |
| sta CURRENT_REV_MASK | |
| clc | |
| lda LINE_ADDRESSES_LSB,y ;y has the y coordinate, load the least significant byte of the address of the middle of screen for the line | |
| adc CURRENT_COL_OFFSET ;Add to the offset for x | |
| sta PLOT_VECTOR | |
| lda LINE_ADDRESSES_MSB,y ;Load the most significant byte of the address of the middle of the screen for the line | |
| adc #0 ;Carry | |
| sta PLOT_VECTOR + 1 ;PLOT_VECTOR now has the address of the byte to write to | |
| ldx #0 | |
| lda (PLOT_VECTOR),x ;Read the previous state of the byte | |
| ora CURRENT_BIT_MASK ;Turn the right pixel on | |
| sta (PLOT_VECTOR),x | |
| clc | |
| lda LINE_ADDRESSES_LSB,y ;y has the y coordinate, load the least significant byte of the address of the middle of screen for the line | |
| sbc CURRENT_COL_OFFSET ;Subtract to the offset for x | |
| sta PLOT_VECTOR | |
| lda LINE_ADDRESSES_MSB,y ;Load the most significant byte of the address of the middle of the screen for the line | |
| sbc #0 ;Carry | |
| sta PLOT_VECTOR + 1 ;PLOT_VECTOR now has the address of the byte to write to | |
| ldx #0 | |
| lda (PLOT_VECTOR),x ;Read the previous state of the byte | |
| ora CURRENT_REV_MASK ;Turn the right pixel on | |
| sta (PLOT_VECTOR),x | |
| rts | |
| plot_symmetries ;plots a point and its transformations by all 8 simple symmetries of the circle | |
| ;x,y | |
| ldx X | |
| clc | |
| lda Y | |
| adc #CY | |
| tay | |
| jsr plot | |
| ;x,-y | |
| ldx X | |
| sec | |
| lda #CY | |
| sbc Y | |
| tay | |
| jsr plot | |
| ;y,x | |
| clc | |
| lda X | |
| adc #CY | |
| tay | |
| ldx Y | |
| jsr plot | |
| ;y,-x | |
| sec | |
| lda #CY | |
| sbc X | |
| tay | |
| ldx Y | |
| jsr plot | |
| rts | |
| org $A200 | |
| ;Display list data (generated using https://bocianu.gitlab.io/fidl/) | |
| display_list | |
| .BYTE $70, $70, $10, $4b, $00, $20, $0b, $0b, $0b, $0b | |
| .BYTE $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b | |
| .BYTE $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b | |
| .BYTE $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b | |
| .BYTE $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b | |
| .BYTE $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b | |
| .BYTE $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b | |
| .BYTE $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b | |
| .BYTE $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b | |
| .BYTE $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b, $0b | |
| .BYTE $0b, $0b, $0b, $0b, $0b, $0b, $41, $00, $a2 | |
| dlistend | |
| pixelmasks | |
| .byte 128,64,32,16,8,4,2,1 | |
| reverse_pixelmasks | |
| .byte 1,2,4,8,16,32,64,128 | |
| ;Cartridge footer | |
| org CARTCS | |
| .word Start ; cold start address | |
| .byte $00 ; 0 == cart exists | |
| .byte $04 ; boot cartridge | |
| .word Start ; start |