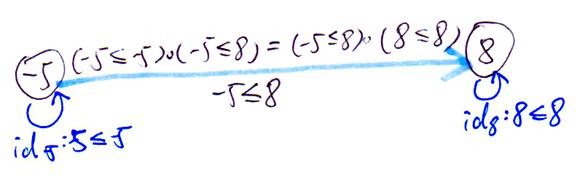Category Theory via C# (1) Fundamentals
[FP & LINQ via C# series]
[Category Theory via C# series]
Category theory is a theoretical framework to describe abstract structures and relations in mathematics, first introduced by Samuel Eilenberg and Saunders Mac Lane in 1940s. It examines mathematical concepts and properties in an abstract way, by formalizing them as collections of items and their relations. Category theory is abstract, and called "general abstract nonsense" by Norman Steenrod; It is also general, therefore widely applied in many areas in mathematics, physics, and computer science, etc. For programming, category theory is the algebraic theory of types and functions, and also the rationale and foundation of LINQ and any functional programming. This chapter discusses category theory and its important concepts, including category, morphism, natural transform, monoid, functor, and monad, etc. These general abstract concepts will be demonstrated with intuitive diagrams and specific C# and LINQ examples. These knowledge also helps building a deep understanding of functional programming in C# or other languages, since any language with types and functions is a category-theoretic structure.
Category and category laws
In category theory, a category C is a algebraic structure consists of the following 3 kinds of mathematical entities:
- A collection of objects, denoted ob(C). This is not the objects in object-oriented programming paradigm.
- A collection of morphisms (relations, aka arrows or maps) between objects, denoted hom(C). A morphism m from source object X to target object Y is denoted m: X → Y.
- A composition operation of morphisms, denoted ∘. For m1: X → Y and m2: Y → Z, their composition is also a morphism (m2∘ m1): Y → Z. Here the name of m1 of m2 also implies the order. m2 ∘ m1 can be read as m2 after m1.


And these entities must satisfy the following 2 category laws:
- Associative law: the composition of morphisms associative: For m1: W → X, m2: X → Y and m3: Y → Z, there is (m3 ∘ m2) ∘ m1≡ ≡ m3 ∘ (m2 ∘ m1).
- Identity law: for each object X, there is an identity morphism: idx : X → X, and identity morphism is neutral for morphism composition. For m: X → Y, there is idY ∘ m ≡ m ≡ m ∘ idX.

To make above abstract definitions intuitive, a category can be represented by the following interface:
public interface ICategory<TObject, TMorphism> { static abstract IEnumerable<TObject> Objects { get; } static abstract TMorphism Compose(TMorphism morphism2, TMorphism morphism1); static abstract TMorphism Id(TObject @object); }
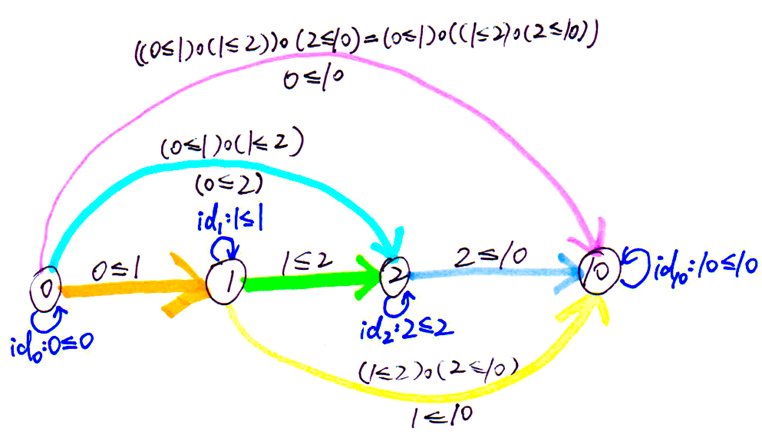
A simple example of category is the category of integers, where the collection of objects are all integers, and the collection of morphisms are ≤ (less than or equal to) relations, from an integer either to itself, or to another integer greater than or equal to it, for example: m1: 0 → 1 (0 ≤ 1), m2: 1 → 10 (1 ≤ 10), etc. Regarding the transitivity of inequality, the ≤ morphisms can be composed, for example, m1: 0 → 1 (0 ≤ 1) and m2: 1 → 10 (1 ≤ 10) can be composed to another morphism (m2 ∘ m1): 0 → 10 (0 ≤ 10).
Apparently, the above composition is associative, foe example: ((1 ≤ 10) ∘ (0 ≤ 1)) ∘ (-1 ≤ 0) ≡ -1 ≤ 10 ≡ (1 ≤ 10) ∘ ((0 ≤ 1) ∘ (-1 ≤ 0)). And for each integer X, there is an identity morphism idX: X → X (X ≤ X), and (Y ≤ Y) ∘ (X ≤ Y) ≡ X ≤ Y ≡ (X ≤ Y) ∘ (X ≤ X). So the category laws are satisfied. In C#, integer can be represented by int, and the morphism of ≤ relation can be represented by a BinaryExpression of node type LessThanOrEqual, so the category can be represented as:
public class Int32Category : ICategory<int, BinaryExpression> { public static IEnumerable<int> Objects { get { for (int int32 = int.MinValue; int32 <= int.MaxValue; int32++) { yield return int32; } } } public static BinaryExpression Compose(BinaryExpression morphism2, BinaryExpression morphism1) => Expression.LessThanOrEqual(morphism2.Left, morphism1.Right); // (Y <= Z) ∘ (X <= Y) => X <= Z. public static BinaryExpression Id(int @object) => Expression.GreaterThanOrEqual(Expression.Constant(@object), Expression.Constant(@object)); // X <= X. }
DotNet category
.NET can also be viewed as a category of types and functions, called DotNet:
- ob(DotNet): the collection of objects in DotNet category are .NET types, like string (System.String), int (System.Int32), bool (System.Boolean), etc.
- hom(DotNet): the collection of morphisms in DotNet category are .NET pure functions between the input type (source object) to the output type (target object), like int.Parse: string → int, DateTime.IsLeapYear: int → bool, etc.
- ∘: in DotNet category, the composition operation of morphisms is the composition of functions.
As already discussed in lambda calculus chapter, function composition is associative, and the unit function Id is the identity morphism:
public static partial class Functions { public static Func<TSource, TResult> o<TSource, TMiddle, TResult>( this Func<TMiddle, TResult> function2, Func<TSource, TMiddle> function1) => value => function2(function1(value)); public static TSource Id<TSource>(T value) => value; }
So that the category laws are satisfied.
The DotNet category can be represented as:
public partial class DotNetCategory : ICategory<Type, Delegate> { public static IEnumerable<Type> Objects => AppDomain.CurrentDomain.GetAssemblies() .SelectMany(assembly => assembly.ExportedTypes); public static Delegate Compose(Delegate morphism2, Delegate morphism1) => // return (Func<TSource, TResult>)Functions.Compose<TSource, TMiddle, TResult>( // (Func<TMiddle, TResult>)morphism2, (Func<TSource, TMiddle>)morphism1); (Delegate)typeof(Tutorial.FuncExtensions).GetMethod(nameof(Tutorial.FuncExtensions.o)) .MakeGenericMethod( // TSource, TMiddle, TResult. morphism1.Method.GetParameters().Single().ParameterType, morphism1.Method.ReturnType, morphism2.Method.ReturnType) .Invoke(null, new object[] { morphism2, morphism1 }); public static Delegate Id(Type @object) => // Functions.Id<TSource> typeof(Functions).GetMethod(nameof(Functions.Id)).MakeGenericMethod(@object) .CreateDelegate(typeof(Func<,>).MakeGenericType(@object, @object)); }
In DotNet category, each object is a type represented by System.Type, so Objects method queries all available types in current assembly, and also recursively query all available assemblies in all reference assemblies. And each morphism is a function from one type to another, which can be represented by System.Delegate, so the composition is just to call the o operator with 2 Delegate instances.