Category Theory via C# (6) Monoidal Functor and Applicative Functor

Monday, December 25, 2023

[FP & LINQ via C# series]

[Category Theory via C# series]

Monoidal functor

Given monoidal categories (C, ⊗, I_C) and (D, ⊛, I_D), a strong lax monoidal functor is a functor F: C → D equipped with:

Monoid binary multiplication operation, which is a natural transformation φ: F(X) ⊛ F(Y) ⇒ F(X ⊗ Y)
Monoid unit, which is a morphism ι: I_D → F(I_C)

F preserves the monoid laws in D:

Associativity law is preserved with D’s associator α_D:
Left unit law is preserved with D’s left unitor λ_D:

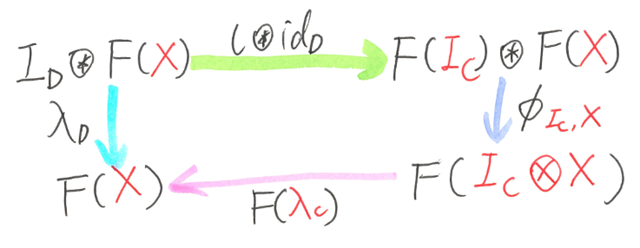
and right unit law is preserved with D’s right unitor ρ_D: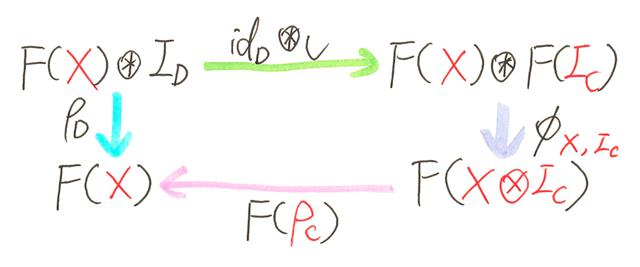

In this tutorial, strong lax monoidal functor is called monoidal functor for short. In DotNet category, monoidal functors are monoidal endofunctors. In the definition, (C, ⊗, I_C) and (D, ⊛, I_D) are both (DotNet, ValueTuple<,>, Unit), so monoidal functor can be IEnumerable<T1>, IEnumerable<T2>defined as:

public interface IMonoidalFunctor<TMonoidalFunctor<>> : IFunctor<TMonoidalFunctor<>>
    where TMonoidalFunctor : IMonoidalFunctor<TMonoidalFunctor<>>
{
    // From IFunctor<TMonoidalFunctor<>>:
    // Select: (TSource -> TResult) -> (TMonoidalFunctor<TSource> -> TMonoidalFunctor<TResult>)
    // Func<TMonoidalFunctor<TSource>, TMonoidalFunctor<TResult>> Select<TSource, TResult>(Func<TSource, TResult> selector);

    // Multiply: TMonoidalFunctor<T1> x TMonoidalFunctor<T2> -> TMonoidalFunctor<T1 x T2>
    // Multiply: ValueTuple<TMonoidalFunctor<T1>, TMonoidalFunctor<T2>> -> TMonoidalFunctor<ValueTuple<T1, T2>>
    TMonoidalFunctor<ValueTuple<T1, T2>> Multiply<T1, T2>(
        ValueTuple<TMonoidalFunctor<T1>, TMonoidalFunctor<T2>> bifunctor);

    // Unit: Unit -> TMonoidalFunctor<Unit>
    TMonoidalFunctor<Unit> Unit(Unit unit);
}

Multiply accepts a ValueTuple<IEnumerable<T1>, IEnumerable<T2>> bifunctor, which is literally a 2-tuple (IEnumerable<T1>, IEnumerable<T2>). For convenience, the explicit ValueTuple<,> parameter can be represented by an implicit tuple, a pair of parameters. So the monoidal functor definition is equivalent to:

public interface IMonoidalFunctor<TMonoidalFunctor<>> : IFunctor<TMonoidalFunctor<>>
    where TMonoidalFunctor : IMonoidalFunctor<TMonoidalFunctor<>>
{
    // Multiply: TMonoidalFunctor<T1> x TMonoidalFunctor<T2> -> TMonoidalFunctor<T1 x T2>
    // Multiply: (TMonoidalFunctor<T1>, TMonoidalFunctor<T2>) -> TMonoidalFunctor<(T1, T2)>
    TMonoidalFunctor<(T1, T2)> Multiply<T1, T2>(
        TMonoidalFunctor<T1> source1, TMonoidalFunctor<T2>> source2); // Unit: Unit

    // Unit: Unit -> TMonoidalFunctor<Unit>
    TMonoidalFunctor<Unit> Unit(Unit unit);
}

IEnumerable<> monoidal functor

IEnumerable<> functor is a monoidal functor. Its Multiply method can be implemented as its extension method:

public static partial class EnumerableExtensions // IEnumerable<T> : IMonoidalFunctor<IEnumerable<>>
{
    // Multiply: IEnumerable<T1> x IEnumerable<T2> -> IEnumerable<T1 x T2>
    // Multiply: ValueTuple<IEnumerable<T1>, IEnumerable<T2>> -> IEnumerable<ValueTuple<T1, T2>>
    // Multiply: (IEnumerable<T1>, IEnumerable<T2>) -> IEnumerable<(T1, T2)>
    public static IEnumerable<(T1, T2)> Multiply<T1, T2>(
        this IEnumerable<T1> source1, IEnumerable<T2> source2) // Implicit tuple.
    {
        foreach (T1 value1 in source1)
        {
            foreach (T2 value2 in source2)
            {
                yield return (value1, value2);
            }
        }
    }

    // Unit: Unit -> IEnumerable<Unit>
    public static IEnumerable<Unit> Unit(Unit unit = default)
    {
        yield return unit;
    }
}

Now extension method Multiply can be used as a infix operator. It can be verified that the above Multiply and Unit implementations preserve the monoid laws by working with associator, left unitor and right unitor of DotNet monoidal category:

// using static Dixin.Linq.CategoryTheory.DotNetCategory;
internal static void MonoidalFunctorLaws()
{
    IEnumerable<Unit> unit = Unit();
    IEnumerable<int> source1 = new int[] { 0, 1 };
    IEnumerable<char> source2 = new char[] { '@', '#' };
    IEnumerable<bool> source3 = new bool[] { true, false };
    IEnumerable<int> source = new int[] { 0, 1, 2, 3, 4 };

    // Associativity preservation: source1.Multiply(source2).Multiply(source3).Select(Associator) == source1.Multiply(source2.Multiply(source3)).
    source1.Multiply(source2).Multiply(source3).Select(Associator).WriteLines();
        // (0, (@, True)) (0, (@, False)) (0, (#, True)) (0, (#, False))
        // (1, (@, True)) (1, (@, False)) (1, (#, True)) (1, (#, False))
    source1.Multiply(source2.Multiply(source3)).WriteLines();
        // (0, (@, True)) (0, (@, False)) (0, (#, True)) (0, (#, False))
        // (1, (@, True)) (1, (@, False)) (1, (#, True)) (1, (#, False))
    // Left unit preservation: unit.Multiply(source).Select(LeftUnitor) == source.
    unit.Multiply(source).Select(LeftUnitor).WriteLines(); // 0 1 2 3 4
    // Right unit preservation: source == source.Multiply(unit).Select(RightUnitor).
    source.Multiply(unit).Select(RightUnitor).WriteLines(); // 0 1 2 3 4
}

How could these methods be useful? Remember functor’s Select method enables selector working with value(s) wrapped by functor:

internal static void Selector1Arity(IEnumerable<int> xs)
{
    Func<int, bool> selector = x => x > 0;
    // Apply selector with xs.
    IEnumerable<bool> applyWithXs = xs.Select(selector);
}

So Select can be viewed as applying 1 arity selector (a TSource –> TResult function) with TFunctor<TSource>. For a N arity selector, to have it work with value(s) wrapped by functor, first curry it, so that it can be viewed as 1 arity function. In the following example, the (T1, T2, T3) –> TResult selector is curried to T1 –> (T2 –> T3 –> TResult) function, so that it can be viewed as only have 1 parameter, and can work with TFunctor<T1>:

internal static void SelectorNArity(IEnumerable<int> xs, IEnumerable<long> ys, IEnumerable<double> zs)
{
    Func<int, long, double, bool> selector = (x, y, z) => x + y + z > 0;

    // Curry selector.
    Func<int, Func<long, Func<double, bool>>> curriedSelector = 
        selector.Curry(); // 1 arity: x => (y => z => x + y + z > 0)
    // Partially apply selector with xs.
    IEnumerable<Func<long, Func<double, bool>>> applyWithXs = xs.Select(curriedSelector);

So partially applying the T1 –> (T2 –> T3 –> TResult) selector with TFunctor<T1> returns TFunctor<T2 –> T3 –> TResult>, where the T2 –> T3 –> TResult function is wrapped by the TFunctor<> functor. To further apply TFunctor<T2 –> T3 –> TResult> with TFunctor<T2>, Multiply can be called:

    // Partially apply selector with ys.
    IEnumerable<(Func<long, Func<double, bool>>, long)> multiplyWithYs = applyWithXs.Multiply(ys);
    IEnumerable<Func<double, bool>> applyWithYs = multiplyWithYs.Select(product =>
    {
        Func<long, Func<double, bool>> partialAppliedSelector = product.Item1;
        long y = product.Item2;
        return partialAppliedSelector(y);
    });

The result of Multiply is TFunctor<(T2 –> T3 –> TResult, T2)>, where each T2 –> T3 –> TResult function is paired with each T2 value, so that each function can be applied with each value, And TFunctor<(T2 –> T3 –> TResult, T2)> is mapped to TFunctor<(T3 –> TResult)>, which can be applied with TFunctor<T3> in the same way:

    // Partially apply selector with zs.
    IEnumerable<(Func<double, bool>, double)> multiplyWithZs = applyWithYs.Multiply(zs);
    IEnumerable<bool> applyWithZs = multiplyWithZs.Select(product =>
    {
        Func<double, bool> partialAppliedSelector = product.Item1;
        double z = product.Item2;
        return partialAppliedSelector(z);
    });
}

So Multiply enables applying functor-wrapped functions (TFunctor<T –> TResult>) with functor-wrapped values (TFunctor<TSource>), which returns functor-wrapped results (TFunctor<TResult>). Generally, the Multiply and Select calls can be encapsulated as the following Apply method:

// Apply: (IEnumerable<TSource -> TResult>, IEnumerable<TSource>) -> IEnumerable<TResult>
public static IEnumerable<TResult> Apply<TSource, TResult>(
    this IEnumerable<Func<TSource, TResult>> selectorWrapper, IEnumerable<TSource> source) =>
        selectorWrapper.Multiply(source).Select(product => product.Item1(product.Item2));

So that the above N arity selector application becomes:

internal static void Apply(IEnumerable<int> xs, IEnumerable<long> ys, IEnumerable<double> zs)
{
    Func<int, long, double, bool> selector = (x, y, z) => x + y + z > 0;
    // Partially apply selector with xs.
    IEnumerable<Func<long, Func<double, bool>>> applyWithXs = xs.Select(selector.Curry());
    // Partially apply selector with ys.
    IEnumerable<Func<double, bool>> applyWithYs = applyWithXs.Apply(ys);
    // Partially apply selector with zs.
    IEnumerable<bool> applyWithZs = applyWithYs.Apply(zs);
}

Applicative functor

A functor, with the above ability to apply functor-wrapped functions with functor-wrapped values, is also called applicative functor. The following is the definition of applicative functor:

// Cannot be compiled.
public interface IApplicativeFunctor<TApplicativeFunctor<>> : IFunctor<TApplicativeFunctor<>>
    where TApplicativeFunctor<> : IApplicativeFunctor<TApplicativeFunctor<>>
{
    // From: IFunctor<TApplicativeFunctor<>>:
    // Select: (TSource -> TResult) -> (TApplicativeFunctor<TSource> -> TApplicativeFunctor<TResult>)
    // Func<TApplicativeFunctor<TSource>, TApplicativeFunctor<TResult>> Select<TSource, TResult>(Func<TSource, TResult> selector);

    // Apply: (TApplicativeFunctor<TSource -> TResult>, TApplicativeFunctor<TSource> -> TApplicativeFunctor<TResult>
    TApplicativeFunctor<TResult> Apply<TSource, TResult>(
        TApplicativeFunctor<Func<TSource, TResult>> selectorWrapper, TApplicativeFunctor<TSource> source);

    // Wrap: TSource -> TApplicativeFunctor<TSource>
    TApplicativeFunctor<TSource> Wrap<TSource>(TSource value);
}

And applicative functor must satisfy the applicative laws:

Functor preservation: applying function is equivalent to applying functor-wrapped function
Identity preservation: applying functor-wrapped identity function, is equivalent to doing nothing.
Composition preservation: functor-wrapped functions can be composed by applying.
Homomorphism: applying functor-wrapped function with functor-wrapped value, is equivalent to functor-wrapping the result of applying that function with that value.
Interchange: when applying functor-wrapped functions with a functor-wrapped value, the functor-wrapped functions and the functor-wrapped value can interchange position.

IEnumerable<> applicative functor

IEnumerable<> functor is a applicative functor. Again, these methods are implemented as extension methods. And for IEnumerable<>, the Wrap method is called Enumerable to be intuitive:

public static partial class EnumerableExtensions // IEnumerable<T> : IApplicativeFunctor<IEnumerable<>>
{
    // Apply: (IEnumerable<TSource -> TResult>, IEnumerable<TSource>) -> IEnumerable<TResult>
    public static IEnumerable<TResult> Apply<TSource, TResult>(
        this IEnumerable<Func<TSource, TResult>> selectorWrapper, IEnumerable<TSource> source)
    {
        foreach (Func<TSource, TResult> selector in selectorWrapper)
        {
            foreach (TSource value in source)
            {
                yield return selector(value);
            }
        }
    }

    // Wrap: TSource -> IEnumerable<TSource>
    public static IEnumerable<TSource> Enumerable<TSource>(this TSource value)
    {
        yield return value;
    }
}

It can be verified that the above Apply and Wrap (Enumerable) implementations satisfy the applicative laws:

internal static void ApplicativeLaws()
{
    IEnumerable<int> source = new int[] { 0, 1, 2, 3, 4 };
    Func<int, double> selector = int32 => Math.Sqrt(int32);
    IEnumerable<Func<int, double>> selectorWrapper1 =
        new Func<int, double>[] { int32 => int32 / 2D, int32 => Math.Sqrt(int32) };
    IEnumerable<Func<double, string>> selectorWrapper2 =
        new Func<double, string>[] { @double => @double.ToString("0.0"), @double => @double.ToString("0.00") };
    Func<Func<double, string>, Func<Func<int, double>, Func<int, string>>> o =
        new Func<Func<double, string>, Func<int, double>, Func<int, string>>(Linq.FuncExtensions.o).Curry();
    int value = 5;

    // Functor preservation: source.Select(selector) == selector.Wrap().Apply(source).
    source.Select(selector).WriteLines(); // 0 1 1.4142135623731 1.73205080756888 2
    selector.Enumerable().Apply(source).WriteLines(); // 0 1 1.4142135623731 1.73205080756888 2
    // Identity preservation: Id.Wrap().Apply(source) == source.
    new Func<int, int>(Functions.Id).Enumerable().Apply(source).WriteLines(); // 0 1 2 3 4
    // Composition preservation: o.Wrap().Apply(selectorWrapper2).Apply(selectorWrapper1).Apply(source) == selectorWrapper2.Apply(selectorWrapper1.Apply(source)).
    o.Enumerable().Apply(selectorWrapper2).Apply(selectorWrapper1).Apply(source).WriteLines();
        // 0.0  0.5  1.0  1.5  2.0
        // 0.0  1.0  1.4  1.7  2.0 
        // 0.00 0.50 1.00 1.50 2.00
        // 0.00 1.00 1.41 1.73 2.00
    selectorWrapper2.Apply(selectorWrapper1.Apply(source)).WriteLines();
        // 0.0  0.5  1.0  1.5  2.0
        // 0.0  1.0  1.4  1.7  2.0 
        // 0.00 0.50 1.00 1.50 2.00
        // 0.00 1.00 1.41 1.73 2.00
    // Homomorphism: selector.Wrap().Apply(value.Wrap()) == selector(value).Wrap().
    selector.Enumerable().Apply(value.Enumerable()).WriteLines(); // 2.23606797749979
    selector(value).Enumerable().WriteLines(); // 2.23606797749979
    // Interchange: selectorWrapper.Apply(value.Wrap()) == (selector => selector(value)).Wrap().Apply(selectorWrapper).
    selectorWrapper1.Apply(value.Enumerable()).WriteLines(); // 2.5 2.23606797749979
    new Func<Func<int, double>, double>(function => function(value)).Enumerable().Apply(selectorWrapper1)
        .WriteLines(); // 2.5 2.23606797749979
}

Monoidal functor vs. applicative functor

The applicative functor definition is actually equivalent to above monoidal functor definition. First, applicative functor’s Apply and Wrap methods can be implemented by monoidal functor’s Multiply and Unit methods:

public static partial class EnumerableExtensions // IEnumerable<T> : IApplicativeFunctor<IEnumerable<>>
{
    // Apply: (IEnumerable<TSource -> TResult>, IEnumerable<TSource>) -> IEnumerable<TResult>
    public static IEnumerable<TResult> Apply<TSource, TResult>(
        this IEnumerable<Func<TSource, TResult>> selectorWrapper, IEnumerable<TSource> source) =>
            selectorWrapper.Multiply(source).Select(product => product.Item1(product.Item2));

    // Wrap: TSource -> IEnumerable<TSource>
    public static IEnumerable<TSource> Enumerable<TSource>(this TSource value) => Unit().Select(unit => value);
}

On the other hand, monoidal functor’s Multiply and Unit methods can be implemented by applicative functor’s Apply and Wrap methods:

public static partial class EnumerableExtensions // IEnumerable<T> : IMonoidalFunctor<IEnumerable<>>
{
    // Multiply: IEnumerable<T1> x IEnumerable<T2> -> IEnumerable<T1 x T2>
    // Multiply: (IEnumerable<T1>, IEnumerable<T2>) -> IEnumerable<(T1, T2)>
    public static IEnumerable<(T1, T2)> Multiply<T1, T2>(
        this IEnumerable<T1> source1, IEnumerable<T2> source2) =>
            new Func<T1, T2, (T1, T2)>(ValueTuple.Create).Curry().Enumerable().Apply(source1).Apply(source2);

    // Unit: Unit -> IEnumerable<Unit>
    public static IEnumerable<Unit> Unit(Unit unit = default) => unit.Enumerable();
}

Generally, for any applicative functor, its (Apply, Wrap) method pair can implement the (Multiply, Unit) method pair required as monoidal functor, and vice versa. This can be virtually demonstrated as:

// Cannot be compiled.
public static class MonoidalFunctorExtensions // (Multiply, Unit) implements (Apply, Wrap).
{
    // Apply: (TMonoidalFunctor<TSource -> TResult>, TMonoidalFunctor<TSource>) -> TMonoidalFunctor<TResult>
    public static TMonoidalFunctor<TResult> Apply<TMonoidalFunctor<>, TSource, TResult>(
        this TMonoidalFunctor<Func<TSource, TResult>> selectorWrapper, TMonoidalFunctor<TSource> source) 
        where TMonoidalFunctor<> : IMonoidalFunctor<TMonoidalFunctor<>> =>
            selectorWrapper.Multiply(source).Select(product => product.Item1(product.Item2));

    // Wrap: TSource -> TMonoidalFunctor<TSource>
    public static TMonoidalFunctor<TSource> Wrap<TMonoidalFunctor<>, TSource>(this TSource value) 
        where TMonoidalFunctor<> : IMonoidalFunctor<TMonoidalFunctor<>> =>TMonoidalFunctor<TSource>
            TMonoidalFunctor<TSource>.Unit().Select(unit => value);
}

// Cannot be compiled.
public static class ApplicativeFunctorExtensions // (Apply, Wrap) implements (Multiply, Unit).
{
    // Multiply: TApplicativeFunctor<T1> x TApplicativeFunctor<T2> -> TApplicativeFunctor<T1 x T2>
    // Multiply: (TApplicativeFunctor<T1>, TApplicativeFunctor<T2>) -> TApplicativeFunctor<(T1, T2)>
    public static TApplicativeFunctor<(T1, T2)> Multiply<TApplicativeFunctor<>, T1, T2>(
        this TApplicativeFunctor<T1> source1, TApplicativeFunctor<T2> source2) 
        where TApplicativeFunctor<> : IApplicativeFunctor<TApplicativeFunctor<>> =>
            new Func<T1, T2, (T1, T2)>(ValueTuple.Create).Curry().Wrap().Apply(source1).Apply(source2);

    // Unit: Unit -> TApplicativeFunctor<Unit>
    public static TApplicativeFunctor<Unit> Unit<TApplicativeFunctor<>>(Unit unit = default)
        where TApplicativeFunctor<> : IApplicativeFunctor<TApplicativeFunctor<>> => unit.Wrap();
}

More Monoidal functors and applicative functors

The Lazy<>, Func<>, Func<T,> functors are also monoidal/applicative functors:

public static partial class LazyExtensions // Lazy<T> : IMonoidalFunctor<Lazy<>>
{
    // Multiply: Lazy<T1> x Lazy<T2> -> Lazy<T1 x T2>
    // Multiply: (Lazy<T1>, Lazy<T2>) -> Lazy<(T1, T2)>
    public static Lazy<(T1, T2)> Multiply<T1, T2>(this Lazy<T1> source1, Lazy<T2> source2) =>
        new Lazy<(T1, T2)>(() => (source1.Value, source2.Value));

    // Unit: Unit -> Lazy<Unit>
    public static Lazy<Unit> Unit(Unit unit = default) => new Lazy<Unit>(() => unit);
}

public static partial class LazyExtensions // Lazy<T> : IApplicativeFunctor<Lazy<>>
{
    // Apply: (Lazy<TSource -> TResult>, Lazy<TSource>) -> Lazy<TResult>
    public static Lazy<TResult> Apply<TSource, TResult>(
        this Lazy<Func<TSource, TResult>> selectorWrapper, Lazy<TSource> source) =>
            selectorWrapper.Multiply(source).Select(product => product.Item1(product.Item2));

    // Wrap: TSource -> Lazy<TSource>
    public static Lazy<T> Lazy<T>(this T value) => Unit().Select(unit => value);
}

public static partial class FuncExtensions // Func<T> : IMonoidalFunctor<Func<>>
{
    // Multiply: Func<T1> x Func<T2> -> Func<T1 x T2>
    // Multiply: (Func<T1>, Func<T2>) -> Func<(T1, T2)>
    public static Func<(T1, T2)> Multiply<T1, T2>(this Func<T1> source1, Func<T2> source2) =>
        () => (source1(), source2());

    // Unit: Unit -> Func<Unit>
    public static Func<Unit> Unit(Unit unit = default) => () => unit;
}

public static partial class FuncExtensions // Func<T> : IApplicativeFunctor<Func<>>
{
    // Apply: (Func<TSource -> TResult>, Func<TSource>) -> Func<TResult>
    public static Func<TResult> Apply<TSource, TResult>(
        this Func<Func<TSource, TResult>> selectorWrapper, Func<TSource> source) =>
            selectorWrapper.Multiply(source).Select(product => product.Item1(product.Item2));

    // Wrap: TSource -> Func<TSource>
    public static Func<T> Func<T>(this T value) => Unit().Select(unit => value);
}

public static partial class FuncExtensions // Func<T, TResult> : IMonoidalFunctor<Func<T,>>
{
    // Multiply: Func<T, T1> x Func<T, T2> -> Func<T, T1 x T2>
    // Multiply: (Func<T, T1>, Func<T, T2>) -> Func<T, (T1, T2)>
    public static Func<T, (T1, T2)> Multiply<T, T1, T2>(this Func<T, T1> source1, Func<T, T2> source2) =>
        value => (source1(value), source2(value));

    // Unit: Unit -> Func<T, Unit>
    public static Func<T, Unit> Unit<T>(Unit unit = default) => _ => unit;
}

public static partial class FuncExtensions // Func<T, TResult> : IApplicativeFunctor<Func<T,>>
{
    // Apply: (Func<T, TSource -> TResult>, Func<T, TSource>) -> Func<T, TResult>
    public static Func<T, TResult> Apply<T, TSource, TResult>(
        this Func<T, Func<TSource, TResult>> selectorWrapper, Func<T, TSource> source) =>
            selectorWrapper.Multiply(source).Select(product => product.Item1(product.Item2));

    // Wrap: TSource -> Func<T, TSource>
    public static Func<T, TSource> Func<T, TSource>(this TSource value) => Unit<T>().Select(unit => value);
}

public static partial class OptionalExtensions // Optional<T> : IMonoidalFunctor<Optional<>>
{
    // Multiply: Optional<T1> x Optional<T2> -> Optional<T1 x T2>
    // Multiply: (Optional<T1>, Optional<T2>) -> Optional<(T1, T2)>
    public static Optional<(T1, T2)> Multiply<T1, T2>(this Optional<T1> source1, Optional<T2> source2) =>
        new Optional<(T1, T2)>(() => source1.HasValue && source2.HasValue
            ? (true, (source1.Value, source2.Value))
            : (false, (default, default)));

    // Unit: Unit -> Optional<Unit>
    public static Optional<Unit> Unit(Unit unit = default) =>
        new Optional<Unit>(() => (true, unit));
}

public static partial class OptionalExtensions // Optional<T> : IApplicativeFunctor<Optional<>>
{
    // Apply: (Optional<TSource -> TResult>, Optional<TSource>) -> Optional<TResult>
    public static Optional<TResult> Apply<TSource, TResult>(
        this Optional<Func<TSource, TResult>> selectorWrapper, Optional<TSource> source) =>
            selectorWrapper.Multiply(source).Select(product => product.Item1(product.Item2));

    // Wrap: TSource -> Optional<TSource>
    public static Optional<T> Optional<T>(this T value) => Unit().Select(unit => value);
}

The ValueTuple<> and Task<> functors are monoidal/applicative functors too. Notice their Multiply/Apply methods cannot defer the execution, and Task<>’s Multiply/Apply methods are impure.

public static partial class ValueTupleExtensions // ValueTuple<T> : IMonoidalFunctor<ValueTuple<>>
{
    // Multiply: ValueTuple<T1> x ValueTuple<T2> -> ValueTuple<T1 x T2>
    // Multiply: (ValueTuple<T1>, ValueTuple<T2>) -> ValueTuple<(T1, T2)>
    public static ValueTuple<(T1, T2)> Multiply<T1, T2>(this ValueTuple<T1> source1, ValueTuple<T2> source2) =>
        new ValueTuple<(T1, T2)>((source1.Item1, source2.Item1)); // Immediate execution.

    // Unit: Unit -> ValueTuple<Unit>
    public static ValueTuple<Unit> Unit(Unit unit = default) => new ValueTuple<Unit>(unit);
}

public static partial class ValueTupleExtensions // ValueTuple<T> : IApplicativeFunctor<ValueTuple<>>
{
    // Apply: (ValueTuple<TSource -> TResult>, ValueTuple<TSource>) -> ValueTuple<TResult>
    public static ValueTuple<TResult> Apply<TSource, TResult>(
        this ValueTuple<Func<TSource, TResult>> selectorWrapper, ValueTuple<TSource> source) =>
            selectorWrapper.Multiply(source).Select(product => product.Item1(product.Item2)); // Immediate execution.

    // Wrap: TSource -> ValueTuple<TSource>
    public static ValueTuple<T> ValueTuple<T>(this T value) => Unit().Select(unit => value);
}

public static partial class TaskExtensions // Task<T> : IMonoidalFunctor<Task<>>
{
    // Multiply: Task<T1> x Task<T2> -> Task<T1 x T2>
    // Multiply: (Task<T1>, Task<T2>) -> Task<(T1, T2)>
    public static async Task<(T1, T2)> Multiply<T1, T2>(this Task<T1> source1, Task<T2> source2) =>
        ((await source1), (await source2)); // Immediate execution, impure.

    // Unit: Unit -> Task<Unit>
    public static Task<Unit> Unit(Unit unit = default) => System.Threading.Tasks.Task.FromResult(unit);
}

public static partial class TaskExtensions // Task<T> : IApplicativeFunctor<Task<>>
{
    // Apply: (Task<TSource -> TResult>, Task<TSource>) -> Task<TResult>
    public static Task<TResult> Apply<TSource, TResult>(
        this Task<Func<TSource, TResult>> selectorWrapper, Task<TSource> source) =>
            selectorWrapper.Multiply(source).Select(product => product.Item1(product.Item2)); // Immediate execution, impure.

    // Wrap: TSource -> Task<TSource>
    public static Task<T> Task<T>(this T value) => Unit().Select(unit => value);
}

It is easy to verify all the above (Multiply, Unit) method pairs preserve the monoid laws, and all the above (Apply, Wrap) method pairs satisfy the applicative laws. However, not any (Multiply, Unit) or any (Apply, Wrap) can automatically satisfy the laws. Take the ValueTuple<T,> functor as example:

public static partial class ValueTupleExtensions // ValueTuple<T1, T2 : IMonoidalFunctor<ValueTuple<T,>>
{
    // Multiply: ValueTuple<T, T1> x ValueTuple<T, T2> -> ValueTuple<T, T1 x T2>
    // Multiply: (ValueTuple<T, T1>, ValueTuple<T, T2>) -> ValueTuple<T, (T1, T2)>
    public static (T, (T1, T2)) Multiply<T, T1, T2>(this (T, T1) source1, (T, T2) source2) =>
        (source1.Item1, (source1.Item2, source2.Item2)); // Immediate execution.

    // Unit: Unit -> ValueTuple<Unit>
    public static (T, Unit) Unit<T>(Unit unit = default) => (default, unit);
}

public static partial class ValueTupleExtensions // ValueTuple<T, TResult> : IApplicativeFunctor<ValueTuple<T,>>
{
    // Apply: (ValueTuple<T, TSource -> TResult>, ValueTuple<T, TSource>) -> ValueTuple<T, TResult>
    public static (T, TResult) Apply<T, TSource, TResult>(
        this (T, Func<TSource, TResult>) selectorWrapper, (T, TSource) source) =>
            selectorWrapper.Multiply(source).Select(product => product.Item1(product.Item2)); // Immediate execution.

    // Wrap: TSource -> ValueTuple<T, TSource>
    public static (T, TSource) ValueTuple<T, TSource>(this TSource value) => Unit<T>().Select(unit => value);
}

The above (Multiply, Unit) implementations cannot preserve the left unit law:

internal static void MonoidalFunctorLaws()
{
    (string, int) source = ("a", 1);
    (string, Unit) unit = Unit<string>();
    (string, int) source1 = ("b", 2);
    (string, char) source2 = ("c", '@');
    (string, bool) source3 = ("d", true);

    // Associativity preservation: source1.Multiply(source2).Multiply(source3).Select(Associator) == source1.Multiply(source2.Multiply(source3)).
    source1.Multiply(source2).Multiply(source3).Select(Associator).WriteLine(); // (b, (2, (@, True)))
    source1.Multiply(source2.Multiply(source3)).WriteLine(); // (b, (2, (@, True)))
    // Left unit preservation: unit.Multiply(source).Select(LeftUnitor) == source.
    unit.Multiply(source).Select(LeftUnitor).WriteLine(); // (, 1)
    // Right unit preservation: source == source.Multiply(unit).Select(RightUnitor).
    source.Multiply(unit).Select(RightUnitor).WriteLine(); // (a, 1)
}

And the above (Apply, Wrap) implementation breaks all applicative laws:

internal static void ApplicativeLaws()
{
    (string, int) source = ("a", 1);
    Func<int, double> selector = int32 => Math.Sqrt(int32);
    (string, Func<int, double>) selectorWrapper1 = 
        ("b", new Func<int, double>(int32 => Math.Sqrt(int32)));
    (string, Func<double, string>) selectorWrapper2 =
        ("c", new Func<double, string>(@double => @double.ToString("0.00")));
    Func<Func<double, string>, Func<Func<int, double>, Func<int, string>>> o = 
        new Func<Func<double, string>, Func<int, double>, Func<int, string>>(Linq.FuncExtensions.o).Curry();
    int value = 5;

    // Functor preservation: source.Select(selector) == selector.Wrap().Apply(source).
    source.Select(selector).WriteLine(); // (a, 1)
    selector.ValueTuple<string, Func<int, double>>().Apply(source).WriteLine(); // (, 1)
    // Identity preservation: Id.Wrap().Apply(source) == source.
    new Func<int, int>(Functions.Id).ValueTuple<string, Func<int, int>>().Apply(source).WriteLine(); // (, 1)
    // Composition preservation: o.Curry().Wrap().Apply(selectorWrapper2).Apply(selectorWrapper1).Apply(source) == selectorWrapper2.Apply(selectorWrapper1.Apply(source)).
    o.ValueTuple<string, Func<Func<double, string>, Func<Func<int, double>, Func<int, string>>>>()
        .Apply(selectorWrapper2).Apply(selectorWrapper1).Apply(source).WriteLine(); // (, 1.00)
    selectorWrapper2.Apply(selectorWrapper1.Apply(source)).WriteLine(); // (c, 1.00)
    // Homomorphism: selector.Wrap().Apply(value.Wrap()) == selector(value).Wrap().
    selector.ValueTuple<string, Func<int, double>>().Apply(value.ValueTuple<string, int>()).WriteLine(); // (, 2.23606797749979)
    selector(value).ValueTuple<string, double>().WriteLine(); // (, 2.23606797749979)
    // Interchange: selectorWrapper.Apply(value.Wrap()) == (selector => selector(value)).Wrap().Apply(selectorWrapper).
    selectorWrapper1.Apply(value.ValueTuple<string, int>()).WriteLine(); // (b, 2.23606797749979)
    new Func<Func<int, double>, double>(function => function(value))
        .ValueTuple<string, Func<Func<int, double>, double>>().Apply(selectorWrapper1).WriteLine(); // (, 2.23606797749979)
}

213 Comments

سکوبندی آزمایشگاه

سکوبندی آزمایشگاه - Tuesday, July 21, 2020 10:43:48 PM

A pedido de amigos os resultados anteriores foram incluídos nesta página.
Deu no poste.
Segunda-Feira 2020 O resultado do jogo do bicho,
deu no poste desta Domingo,
segue abaixo para apuração.
Pesquise sempre por
“jogo do bicho portalbrasil.

Deu no Poste - Sunday, August 23, 2020 8:13:13 AM

Amazon.com/mytv - enter the 6 digit amazon mytv code you receive at screen at www.amazon.com/mytv to regiter your device. contact amazon support for hel

www.amazon.com/mytv - Monday, October 26, 2020 10:23:00 PM

good post

سایت بتکارت - Tuesday, February 16, 2021 6:59:54 AM

This article is really fantastic and thanks for sharing the valuable post.

Free Astrology Consultancy Advice Online - Thursday, April 22, 2021 11:29:06 PM

awesome post. I’m a normal visitor of your web site and appreciate you taking the time to maintain the nice site. I’ll be a frequent visitor for a long time.

Sifli Ilm Black Magic Spells - Friday, April 23, 2021 2:46:35 AM

Thanks for sharing.I found a lot of interesting information here. A really good post, very thankful and hopeful that you will write many more

Husband Wife Love Problem Solution in india - Friday, April 23, 2021 3:16:25 AM

Great Article it its really informative and innovative keep us posted with new updates. its was really valuable.

Black Magic Astrologers - Friday, April 23, 2021 3:30:25 AM

Thanks for writing such a good article, I stumbled onto your blog and read a few post. I like your style of writing...

Online Love Solutions - Friday, April 23, 2021 3:54:18 AM

Great Post !! Very interesting topic will bookmark your site to check if you write more about in the future.

Husband wife love problem solution - Friday, April 23, 2021 4:21:12 AM

Very interesting topic will bookmark your site to check if you Post more about in the future.

Free Astrology Consultancy Advice Online - Friday, April 23, 2021 4:37:43 AM

Thanks for share amazing content. Very interesting keep posting.

Islamic dua for Love back - Friday, April 23, 2021 5:01:51 AM

کلینیک لیزر شفا به عنوان بهترین مرکز درمان بیماری های گوارشی و نشیمن گاهی با مدیریت دکتر داود تاج بخش در رابطه با بیماریهای ناحیه مقعد خدماتی از جمله درمان بیماری هایی مثل هموروئید، فیستول، شقاق ارائه می دهد. کلینیک لیزر شفا فقط و فقط بر روی بیماری های مقعدی تمرکز داشته و تمامی متخصصین در این رابطه دور هم گرد آورده است.
https://laser-doc.com/

بهترین مرکز درمان بیماری های گوارشی و نشیمن گاهی - Saturday, May 15, 2021 1:15:47 AM

Walmart Giftcard Balance | Check Walmart Gift Card Balance is actively using the technology Domain Not Resolving for its website, according to BuiltWith.

walmart gift card balance - Monday, June 7, 2021 12:06:47 AM

Very attractive blog with amazing informations.

mariyam - Wednesday, June 16, 2021 8:59:41 AM

This post is really astounding one! I was delighted to read this, very much useful. Many thanks

geometry dash unblocked - Tuesday, June 22, 2021 1:15:34 AM

Hey! Someone in my Myspace group shared this website with us so I came to look it over.
I'm definitely loving the information. I'm book-marking and will be
tweeting this to my followers! Exceptional blog and great
style and design.

oncasinosite - Friday, July 16, 2021 4:11:18 AM

Great looking web site. Assume you did a lot of your very own html coding.

casinositewin - Friday, July 16, 2021 4:12:27 AM

Hi there, just wanted to tell you, I liked this article. It was inspiring.
Keep on posting!

toto365pro - Friday, July 16, 2021 4:12:53 AM

Great internet site! It looks very expert! Keep up the
good work!

sportstototop - Friday, July 16, 2021 4:13:30 AM

OMG this game deserves to be played by the whole world.

friday night funkin - Thursday, July 22, 2021 12:50:07 AM

I got such a useful stuff on your website that helps me a lot to gain information.

Vedic astrology predictions - Thursday, July 29, 2021 1:21:53 AM

Very nice post. Every day from distinct blogs, I learn something different.

Husband wife problem solution - Thursday, July 29, 2021 1:55:59 AM

Thank you so much for sharing your thoughts. This is exactly what I needs.

Mantra to attract Love - Thursday, July 29, 2021 2:16:11 AM

I am very glad that I am one of the visitors of this great website.

Online Vashikaran Specialist bengali Baba Ji - Thursday, July 29, 2021 2:34:00 AM

Daily I visit most of the web pages to get new stuff. But here I got something unique and informative.

Love Marriage Problem Solutions online - Thursday, July 29, 2021 2:51:04 AM

Very energetic post! Everyone is searching for the wonderful stuff.

Dua For Parents - Thursday, July 29, 2021 3:08:43 AM

I am very glad that I am one of the visitors of this great website.

How To Get My Ex Boyfriend Back - Thursday, July 29, 2021 3:26:43 AM

Daily I visit most of the web pages to get new stuff. But here I got something unique and informative.

Lottery Number Specialist - Thursday, July 29, 2021 3:42:00 AM

This is the one of the most important information for me. And I am feeling glad reading your article. The article is really excellent ?

Islamic astrologer - Thursday, July 29, 2021 10:00:24 PM

It helps to get more knowledge about this topic. I really appreciate your effort that you put to provide such great article.

Islamic dua for Love back - Thursday, July 29, 2021 10:23:10 PM

Your website always shares such an useful information that I was looking for.

Get My Love Back in Australia Baba Ji - Thursday, July 29, 2021 10:40:21 PM

Thank you so much for sharing your thoughts. This is exactly what I needs.

Love Spells - Thursday, July 29, 2021 11:04:19 PM

Your website contains such useful information. Appreciate your written skills and your blog.

Photography Services company in jaipur - Friday, July 30, 2021 2:18:00 AM

This formula that you for all intents and purposes are presenting seems rigid to me, since basically your previous research essentially was definitely promising to me.

강남가라오케 - Tuesday, November 30, 2021 12:24:23 AM

https://ma-study.blogspot.com/

medicalphd - Monday, December 13, 2021 11:21:50 AM

If you are writing your dissertation, thesis report, or any other paper and don't know what material to put into it? visit Dissertation Writing Help & get the best assistance from our expert writers on board.

Masters Dissertation Proposal Help - Tuesday, April 12, 2022 10:40:29 PM

Friday Night Funkin is a game created by ninja_muffin99 and some others. This game is brought to life by the music contained in this game. It has simple gameplay but very difficult to win.

FNF - Saturday, May 7, 2022 11:29:19 AM

KBH games is a game website with the highest quality and fastest speed today. It meets many of the standards you need, Here we are constantly updating many new games that you should try it now.

kbh games - Saturday, May 7, 2022 11:30:24 AM

following caused error anyone help!
public static partial class TaskExtensions // Task<T> : IMonoidalFunctor<Task<>>
{
// Multiply: Task<T1> x Task<T2> -> Task<T1 x T2>
// Multiply: (Task<T1>, Task<T2>) -> Task<(T1, T2)>

طراحی مطب - Wednesday, May 18, 2022 11:42:16 PM

برخی از بازی های شرکت بلیزارد بصورت رایگان دردسترس گیمرها و کاربران نخواهد بود. و این کاربران برای استفاده از بازی گیم تایم یا همان گیم کارت خریداری کنند. یکی از این بازی ها،‌ بازی محبوب و پرطرفدار ورلدآف وارکرافت است. به شارژ ماهیانه بازی وارکرافت در سرورهای بازی بلیزارد گیم تایم می گویند ، که در فروشگاه جت گیم موجود می باشد.

خرید گیم تایم 60 روزه ازفروشگاه جت گیم:

در واقع گیم تایم 60 روزه نمونه ای جدید است از گیم تایم ها برای استفاده دربازی World of Warcraft . که در ادامه بیشتر در مورد این محصول و نحوه استفاده از آن توضیح می دهیم .

شما با خرید گیم تایم 60 روزه در مدت زمان آن گیم تایم ( 60 روز ) به امکاناتی در بازی World of Warcraft درسترسی پیدا خواهید کرد که این امکانات شامل موارد زیر میباشند :

1 - اجازه لول آپ کردن تا لول 50 ( بدون گیم تایم فقط می توانید تا لول 20 بازی کنید )

2 - اجازه چت کردن با دیگران درون بازی ( بدون گیم تایم نمی توانید در بازی چت کنید )

3 - دسترسی به بازی World of Warcraft Classic

در نتیجه برای بازی در World of Warcraft حتمآ به تهیه گیم تایم نیاز دارید.

نکته 1 : گیم تایم یا همان زمان بازی ورد اف وارکرفت برای توانایی انلاین بازی کردن استفاده می شود و بدون گیم تایم امکان بازی کردن بازی محبوب ورد اف وارکرفت را نخواهید داشت.

نکته 2 : درصورتی که گیم تایم نداشته باشید امکان بازی ورد اف وارکرفت کلاسیک را ندارید و شما میتوانید جهت خرید این محصول از وبسایت ما اقدام نمایید

نکته 3 : نیازی به وارد کردن مشخصات اکانت بلیزارد شما نمی باشد زیرا کد گیم تایم توسط خود شما و پس از دریافت کد، وارد می شود ( آموزش وارد کردن در پایین صفحه قرار دارد )

https://jetgames.ir - Friday, May 27, 2022 1:40:09 AM

برخی از بازی های شرکت بلیزارد بصورت رایگان دردسترس گیمرها و کاربران نخواهد بود. و این کاربران برای استفاده از بازی گیم تایم یا همان گیم کارت خریداری کنند. یکی از این بازی ها،‌ بازی محبوب و پرطرفدار ورلدآف وارکرافت است. به شارژ ماهیانه بازی وارکرافت در سرورهای بازی بلیزارد گیم تایم می گویند ، که در فروشگاه جت گیم موجود می باشد.

خرید گیم تایم 60 روزه ازفروشگاه جت گیم:

در واقع گیم تایم 60 روزه نمونه ای جدید است از گیم تایم ها برای استفاده دربازی World of Warcraft . که در ادامه بیشتر در مورد این محصول و نحوه استفاده از آن توضیح می دهیم .

شما با خرید گیم تایم 60 روزه در مدت زمان آن گیم تایم ( 60 روز ) به امکاناتی در بازی World of Warcraft درسترسی پیدا خواهید کرد که این امکانات شامل موارد زیر میباشند :

1 - اجازه لول آپ کردن تا لول 50 ( بدون گیم تایم فقط می توانید تا لول 20 بازی کنید )

2 - اجازه چت کردن با دیگران درون بازی ( بدون گیم تایم نمی توانید در بازی چت کنید )

3 - دسترسی به بازی World of Warcraft Classic

در نتیجه برای بازی در World of Warcraft حتمآ به تهیه گیم تایم نیاز دارید.

نکته 1 : گیم تایم یا همان زمان بازی ورد اف وارکرفت برای توانایی انلاین بازی کردن استفاده می شود و بدون گیم تایم امکان بازی کردن بازی محبوب ورد اف وارکرفت را نخواهید داشت.

نکته 2 : درصورتی که گیم تایم نداشته باشید امکان بازی ورد اف وارکرفت کلاسیک را ندارید و شما میتوانید جهت خرید این محصول از وبسایت ما فروشگاه جت گیم اقدام نمایید

https://jetgames.ir - Monday, June 6, 2022 12:10:22 PM

Very good content. I appreciate your writing skills.

Friday Night Funkin - Monday, June 13, 2022 9:42:09 AM

<a href="https://pg-slot.game/%e0%b8%9a%e0%b8%a3%e0%b8%b4%e0%b8%81%e0%b8%b2%e0%b8%a3/pgslot/%e0%b9%82%e0%b8%9a%e0%b8%99%e0%b8%b1%e0%b8%aa-pgslot-%e0%b9%84%e0%b8%94%e0%b9%89%e0%b9%80%e0%b8%87%e0%b8%b4%e0%b8%99%e0%b8%a1%e0%b8%b2%e0%b8%81%e0%b8%81%e0%b8%a7%e0%b9%88%e0%b8%b2%e0%b8%96%e0%b8%b9%e0%b8%81-%e0%b8%ab%e0%b8%a7%e0%b8%a2/">โบนัส Pgslot ได้เงินมากกว่าถูก หวย</a> เล่นเกม Pgslot มีให้ลุ้นทุกวันทุกเวลาไม่ต้องรอเหมือนหวย Pgslot มีเกมภาพสวยๆมากมาย นักเสี่ยงโชคไม่ควรพลาด

jonny - Thursday, June 16, 2022 7:14:45 AM

veru good
thank you so much

affiliatblogger.com - Sunday, June 19, 2022 5:29:44 AM

I used to visit this site every weekend because it actually contributes this interesting material.

<a href="https://www.sportstotolink.com/" ="_blank" title="토토사이트">토토사이트</a>

sportstotolink - Thursday, June 30, 2022 5:08:35 AM

Praise my father for this weblog, which is actually surprising.

https://www.totositeweb.com

totositeweb.com - Thursday, June 30, 2022 5:11:11 AM

Write more, that all I have to say. Literally, it seems as though you relied on the video to make your point. You definitely know what your talking about, why throw away your intelligence on just posting videos to your weblog when you could be giving us something informative to read?

https://www.wooricasino.top

wooricasino - Thursday, June 30, 2022 5:15:27 AM

I hope you will be happy when you plan something in the long run in perfect time is perfect. You can ask questions or advice that you are interested in, and learn about this post Perhaps you could write a follow-up article about this article. I even want to learn more about it!

https://www.baccaratsite.win

baccaratsite.win - Thursday, June 30, 2022 5:17:50 AM

Great is what I give praise for FNAF (one of the most attractive horror games) today.

fnaf - Monday, July 4, 2022 11:15:31 AM

It's great to participate in Wordle game, which is a good and good word guessing game hidden in crosswords for players. Have you ever been to this game?

wordle game - Monday, July 4, 2022 11:17:46 AM

First of all, thank you for your post. Keo nha cai Your posts are neatly organized with the information I want, so there are plenty of resources to reference. I bookmark this site and will find your posts frequently in the future. Thanks again ^^

Keo nha cai - Saturday, July 30, 2022 6:39:45 PM

Being here with everyone is fantastic, and I value you sharing your knowledge with me. I sincerely appreciate the insight and details you have shared here.

fnf - Sunday, August 14, 2022 9:44:54 PM

The best pitch deck your prospects have ever seen can help you land new business. So select one of our Pitch Deck Templates and effortlessly customise it to make it even more alluring.

Deck Designers - Monday, August 15, 2022 6:12:25 AM

It's too bad to check your article late. I wonder what it would be if we met a little faster. I want to exchange a little more, but please visit my site Keonhacai and leave a message!!

Keonhacai - Tuesday, August 16, 2022 6:47:10 PM

Do you want to participate in the Wordle game? Please visit our website. It's free.

wordle online - Monday, August 22, 2022 10:43:46 AM

Your writing is perfect and complete. casino online However, I think it will be more wonderful if your post includes additional topics that I am thinking of. I have a lot of posts on my site similar to your topic. Would you like to visit once?

casino online - Sunday, September 4, 2022 11:40:05 PM

To maintain a healthy lifestyle, it would be preferable if you made significant adjustments, but change does not occur unless you put in a lot of effort. I'm here to help you make that shift. Our Virtual Health Coaches are here to assist you in reaching your goals and getting the outcomes you desire. Since you are currently on the right page, you can stop looking for a health coach nearby.

Virtual Health Coaches - Wednesday, September 14, 2022 2:22:15 AM

I saw your article well. You seem to enjoy majorsite for some reason. We can help you enjoy more fun. Welcome anytime :-)

majorsite - Sunday, September 18, 2022 9:44:30 PM

The post will add value and are meaningful, useful additions to a post.

Isher - Monday, September 19, 2022 11:47:10 PM

I have been looking for articles on these topics for a long time. I don't know how grateful you are for posting on this topic. Thank you for the numerous articles on this site, I will subscribe to those links in my bookmarks and visit them often. Have a nice day

casinocommunity - Sunday, October 2, 2022 6:46:44 PM

Say, you got a nice blog article. Really thank you! Really Cool. This was really an interesting topic and I kinda agree with what you have mentioned here!

sportstotomen - Sunday, October 9, 2022 9:10:40 PM

Thanks so much for this post, pretty worthwhile material.

gostopsite - Sunday, October 9, 2022 9:11:25 PM

Thanks for the useful information. It's more informative and easy to understand. Please help me suggest CBSE

19guide03 - Sunday, October 9, 2022 9:12:00 PM

Thanks in favor of sharing such a nice idea, paragraph is good, thats why i have read it fully.

casinosite - Sunday, October 9, 2022 9:12:41 PM

This is one of the very interesting posts. I like the way you write. I'll bookmark it and visit it from time to time to read it. Thank you very much.

메이저토토 - Thursday, October 13, 2022 11:10:57 PM

The Logo Castle is where your fantasies work out as expected and your business achievement makes the biggest difference. We cover every one of the areas to ensure that you won't require some other advanced promoting organization administrations supplier.

Digital Marketing Agency Services - Wednesday, October 19, 2022 11:21:57 PM

Your blog has some of the best stuff, and I adore reading it.

Smallest Bluetooth Earbuds - Thursday, October 20, 2022 12:15:45 AM

Really a great post. The topic you discuss is so inspiring and motivating. Thank you for the share..

casinoday.one - Sunday, October 30, 2022 7:41:18 PM

Absolutely love all your blogs and enjoy reading the “story’ behind each. Can’t thank you enough! Keep up the amazing work…

casinolink.xyz - Sunday, October 30, 2022 7:41:56 PM

I personally appreciate your work. I’m quite new in this field. And I want to say thanks for the great info.. Please add more post.

casinomarket.xyz - Sunday, October 30, 2022 7:42:22 PM

Cool stuff you have got and you keep update all of us.

casinonori.xyz - Sunday, October 30, 2022 7:42:49 PM

Thanks for your post. I’ve been thinking about writing a very comparable post over the last couple of weeks, I’ll probably keep it short and sweet and link to this instead if thats cool. Thanks.

casinonoriter.xyz - Sunday, October 30, 2022 7:43:16 PM

Just about each amazing really own & each methods to your website are extraordinary

chucheon.xyz - Sunday, October 30, 2022 7:43:42 PM

I’m definitely going to look into your other post. Really very useful tips are provided here. Thank you so much and please keep up the good job.

easybetting.xyz - Sunday, October 30, 2022 7:44:13 PM

I am mainly passionate about your outstanding achieve

easytoto.xyz - Sunday, October 30, 2022 7:44:47 PM

I was surfing net and fortunately came across this site and found very interesting stuff here. Its really fun to read. I enjoyed a lot. Thanks for sharing this wonderful information.

hellototo.xyz - Sunday, October 30, 2022 7:45:41 PM

Great article and excellent layout. Your blog post deserves all of the positive feedback it’s been getting.

highposition.xyz - Sunday, October 30, 2022 7:46:28 PM

I certainly suggested your publishing design and how you weblink your ideas

슬롯머신 - Sunday, October 30, 2022 7:47:09 PM

You always come up with helpful and timely information. I will take this information and add your site to my list. Cheers!

토토 - Sunday, October 30, 2022 7:47:45 PM

I really fascinated by this excellent blog, thanks for such wonderful blog! Good job and more power!

스포츠중계 - Sunday, October 30, 2022 7:48:28 PM

Benefits it a lot for developing incredible articles its effective for us

스포츠토토 - Sunday, October 30, 2022 7:49:10 PM

The assignment submission period was over and I was nervous, and I am very happy to see your post just in time and it was a great help. Thank you ! Leave your blog address below. Please visit me anytime.

bitcoincasino - Thursday, November 10, 2022 8:39:07 PM

Your blog has probably the best stuff, and I revere understanding it.

Multifamily Social Media - Monday, November 14, 2022 12:39:47 AM

A content that gives users a lot of valuable information.

wordle website - Monday, November 28, 2022 8:19:31 AM

principle of your idea it makes you perfect and i like this idea. Thank you for always producing your work for me to read.

โปรโมทชั่น DG Casino - Monday, January 9, 2023 8:52:32 PM

خرید دراگون فلایت بیس ( نسخه پایه) سری بازی ورلد آف وارکرافت یکی از قدیمی ترین گیم هایی است که هم از نظر محبوبیت و هم از نظر شکل بازی نزدیک به دو دهه است که با ارائه انواع بسته های الحاقی برای دوستداران این گیم سرپا است و به کار خود ادامه می دهد.ورلد آف وارکرافت توسط شرکت بلیزارد ارائه شده و بدلیل سبک بازی و گرافیک بالا در سرتاسر جهان طرفداران زیادی را به خود جذب کرده است.
این بازی محبوب دارای انواع بسته های الحاقی میباشد که جدید ترین آن که به تازگی رونمائی شده و در حال حاضر صرفا امکان تهیه پیش فروش آن فراهم میباشد دراگون فلایت است

shahini - Wednesday, February 8, 2023 2:02:07 AM

It's a very interesting formula. I absolutely adore <a href="https://popmovie888.com/movie/taken-2-%e0%b9%80%e0%b8%97%e0%b8%84%e0%b9%80%e0%b8%84%e0%b8%99-2-%e0%b8%85%e0%b8%99%e0%b8%84%e0%b8%a1-%e0%b8%a5%e0%b9%88%e0%b8%b2%e0%b9%84%e0%b8%a1%e0%b9%88%e0%b8%a2%e0%b8%b1%e0%b9%89%e0%b8%87-2012/" rel="bookmark" title=" ดูTaken 2 เทคเคน 2 ฅนคม ล่าไม่ยั้ง "> ดูTaken 2 เทคเคน 2 ฅนคม ล่าไม่ยั้ง </a>

ดูหนังออนไลน์ - Saturday, February 18, 2023 12:46:07 AM

It's very exciting. I just read this article for the first time, thanks for sharing, thank you.<a href="https://popmovie888.com/" rel="bookmark" title="หนังออนไลน์ 2023 พากย์ไทย">หนังออนไลน์ 2023 พากย์ไทย</a>

หนังใหม่พากย์ไทย - Saturday, February 25, 2023 1:44:59 AM

It's very exciting. I just read this article for the first time, thanks for sharing, thank you.<a href="https://popmovie888.com/" rel="bookmark" title=" ดูหนังออนไลน์พากย์ไทยเต็มเรื่อง "> ดูหนังออนไลน์พากย์ไทยเต็มเรื่อง </a>

หนังออนไลน์พากย์ไทยเต็มเรื่อง - Saturday, February 25, 2023 4:49:54 AM

Can you tell us more about this? I’d want to find out some additional information. <a href="https://mtnamsan.com/" target="_blank">먹튀검증</a>

먹튀검증 - Monday, March 6, 2023 11:04:41 PM

I at last got the opportunity to peruse this phenomenal substance. It is both exceptionally intriguing and instructive. I'm sure that each and every individual who read it has quite far to go.

Townhouses For Sale In Dubai - Tuesday, March 7, 2023 3:42:24 AM

This post is truly nice and I have learned lot of things from it concerning blogging.

ล้างรถอุบล - Saturday, March 25, 2023 1:08:42 AM

In termini di privacy, Alice Mail offre la possibilità di impostare un codice PIN per proteggere l'accesso alla propria email su dispositivi mobili. Inoltre, gli utenti possono impostare la cancellazione automatica delle email dopo un certo periodo di tempo, garantendo una maggiore privacy e sicurezza.

alice mail - Tuesday, April 11, 2023 4:58:03 AM

I at last got the opportunity to peruse this phenomenal substance. It is both exceptionally intriguing and instructive. I'm sure that each and every individual who read it has quite far to go.

اهنگ جدید - Monday, April 17, 2023 2:46:49 PM

very nice blog thanks for sharing *_*

اهنگ موزیک ترین - Wednesday, May 3, 2023 11:20:28 PM

blog online journals are effectively open and very edifying so continue doing the astounding work folks :) <a href="https://totomachine.com/" target="_blank">먹튀검증</a>

토토사이트 - Sunday, May 14, 2023 11:17:15 AM

Please read it in detail as the details and the expiry of your plan will be provided in it. So from now, you can watch every movie and show released on Disney.

Disneyplus/begin - Wednesday, July 5, 2023 3:31:17 AM

how do you You think of a lot of content. And it's great.

เว็บหวยหุ้นจีน - Friday, July 28, 2023 8:07:12 PM

ok

nipaco - Friday, August 4, 2023 3:53:55 AM

I JUST ADDED THIS SITE TO MY GOOGLE READER, EXCELLENT STUFF. CAN’T GET ENOUGH!

spo8rtst31otototop - Wednesday, August 30, 2023 7:34:16 PM

I DO BELIEVE ALL OF THE CONCEPTS YOU HAVE INTRODUCED IN YOUR POST. THEY’RE VERY CONVINCING AND WILL DEFINITELY WORK.

pah8ink31osite - Wednesday, August 30, 2023 7:34:48 PM

THE POSTS ARE VERY QUICK FOR NEWBIES. THANK YOU FOR THE POST!

race8si31te - Wednesday, August 30, 2023 7:35:12 PM

THANKS FOR THE INFORMATION.

baca8ra31site - Wednesday, August 30, 2023 7:36:58 PM

Thank you for the information regarding coding, I read it and it is easy to understand and will be useful.

123bet - Thursday, September 7, 2023 9:00:06 PM

i like your article I look forward to receiving new news from you every day. I have received your news. i will follow you And hope to continue to receive interesting stories like this.

ติดต่อ sa - Wednesday, September 13, 2023 9:30:10 PM

Tak mungkin kamu menemukan situs terbaik selain di <a href="https://bursa188.pro/"rel="dofollow">BURSA188</a> <a href="https://bursa188.store/"rel="dofollow">BURSA188</a>

BURSA188 - Saturday, September 23, 2023 2:17:31 AM

به سبک آقای پیشرفت یاد میگیری به موفقیت در کسب و کار و زندگی برسی
https://aghayepishraft.com/

آقای پیشرفت - Friday, September 29, 2023 1:06:34 AM

You have truly helped thousands of people who come to your the blog and give them valuable details. Thank you for sharing with us.

ออมสิน สลาก - Tuesday, October 10, 2023 12:06:56 AM

I appreciate your post. Every day I look forward to hearing from you with new information. I have heard from you. I'll follow you in the hopes of seeing more intriguing posts like this.

autobiography writing services - Thursday, October 19, 2023 7:10:57 AM

I am so glad that you shared this useful information with us.

กีฬา คลิปโต - Monday, November 6, 2023 9:19:10 PM

I've been looking for photos and articles on this topic over the past few days due to a school assignment, <a href="https://maps.google.cd/url?sa=t&url=https%3A%2F%2Fwww.mtclean.blog/">casinocommunity</a> and I'm really happy to find a post with the material I was looking for! I bookmark and will come often! Thanks :D

casinocommunity - Wednesday, November 22, 2023 12:06:27 AM

I've been troubled for several days with this topic. <a href="https://maps.google.cat/url?sa=t&url=https%3A%2F%2Fwww.mtclean.blog/">majorsite</a>, But by chance looking at your post solved my problem! I will leave my blog, so when would you like to visit it?

majorsite - Wednesday, November 22, 2023 12:06:55 AM

The assignment submission period was over and I was nervous, <a href="https://maps.google.ca/url?sa=t&url=https%3A%2F%2Fwww.mtclean.blog/">bitcoincasino</a> and I am very happy to see your post just in time and it was a great help. Thank you ! Leave your blog address below. Please visit me anytime.

bitcoincasino - Wednesday, November 22, 2023 12:07:23 AM

I am very impressed with your writing <a href="https://maps.google.by/url?sa=t&url=https%3A%2F%2Fwww.mtclean.blog/">safetoto</a> I couldn't think of this, but it's amazing! I wrote several posts similar to this one, but please come and see!

safetoto - Wednesday, November 22, 2023 12:07:57 AM

Great codes

arta - Wednesday, December 27, 2023 1:17:17 AM

The codes are very beautiful

arta - Wednesday, December 27, 2023 1:33:38 AM

I really appreciate how you connect the theoretical dots with actual code snippets. It's like you're a guide in the world of category theory, showing us not just the landscapes but also the practical paths to navigate them. Your approach to using C# to illustrate these concepts is a game-changer for those of us trying to bridge the gap between theory and implementation.

Armanunderpin - Wednesday, December 27, 2023 9:06:49 PM

goode line

reza - Saturday, January 6, 2024 2:34:21 AM

Pavzi.com is a startup by passionate webmasters and bloggers who have a passion for providing engaging content that is accurate, interesting, and worthy to read. https://pavzi.com/ We are more like a web community where you can find different information, resources, and topics on day-to-day incidents or news. We provide you with the finest web content on every topic possible with the help of the editorial and content team.

pavzi.com - Thursday, January 18, 2024 11:38:27 PM

lavagame <a href="https://www.lava678.asia" rel="nofollow ugc"> lavagame </a> เว็บตรงสล็อตที่กำลังได้รับความนิยมในประเทศไทย การเลือกเล่นเกมสล็อตออนไลน์ได้รับความนิยมเพิ่มขึ้นในประเทศไทย <a href="https://www.lava678.asia" rel="nofollow ugc"> สล็อตเว็บตรง </a> สมัคร ปั่นสล็อต ทดลองปั่นสล็อต

lava678 - Sunday, January 21, 2024 12:46:05 AM

I appreciate your meticulous research and the clarity with which you present complex ideas. Your writing not only informs but also captivates the reader's attention. The real-world examples you provide make the content relatable and applicable.

DevOps Tutorial - Tuesday, January 30, 2024 4:52:54 AM

Such an amazing and helpful post this is. I really really love it. It’s so good and so awesome.

안전한 파워볼사이트 - Monday, February 19, 2024 2:00:04 AM

Hard to ignore such an amazing article like this. You really amazed me with your writing talent.

안전 토토사이트 - Monday, February 19, 2024 2:02:15 AM

Your website is really cool and this is a great inspiring article. Thank you so much

온라인카지노사이트 - Monday, February 19, 2024 2:04:14 AM

Excellent information on your blog, thank you for taking the time to share with us.

토토사이트 추천 - Monday, February 19, 2024 2:06:09 AM

I was looking it for so long , and i found it finally that i know it will help me .

실시간 바카라사이트 - Monday, February 19, 2024 2:08:32 AM

I am always searching online for storys that can accommodate me.

안전 토토사이트 - Monday, February 19, 2024 2:10:48 AM

<a href="https://www.Miami900.com/" rel="nofollow ugc">Miami900</a>

MIAMI900 (https://heylink.me/Miami900/)
คาสิโน ออนไลน์ เป็นเว็บไซต์อันดับ 1 ของประเทศไทย สำหรับคนที่ชอบเล่นคาสิโน ออนไลน์และสล็อต ออนไลน์ เป็นเว็บพนันที่ดีที่สุดอย่าง MIAMI900 รวมของเกมคาสิโนและสล็อต ออนไลน์ต่างๆ ยอดฮิตมากมาย เช่น บาคาร่า เสือมังกร รูเล็ต แบล็คแจ็ค สล็อต และเกมอื่นๆ อีกมากมาย ให้ท่านสามารถเลือกเล่นได้ตามที่ต้องการ อย่างสนุกสนาน คาสิโน ออนไลน์ที่ดีที่สุด และ ครบวงจร มากที่สุด เต็มไปด้วยเกมคาสิโนและสล็อต ออนไลน์ มีระบบธุรกรรมการเงินที่มั่นคง ด้วยระบบฝาก - ถอนอัตโนมัติ

MIAMI900 - Monday, February 26, 2024 8:44:52 AM

I definitely enjoying every little bit of this blog. It is a great website and nice share. I want to thank you. Good job! You guys do a great blog, and have some great contents. Keep up the good work <a href="https://www.healing4me.co.kr/">1인샵</a>

1인샵 - Saturday, March 2, 2024 6:16:22 AM

The post is written in very a good manner and it contains many useful information for me.

스포츠중계 - Wednesday, March 6, 2024 11:23:36 PM

I am overwhelmed by your post with such a nice topic. Usually I visit your blogs and get updated through the information you include but today’s blog would be the most appreciable. Well done <a href="https://mt-super.com/">먹튀검증</a>

먹튀검증 - Monday, March 11, 2024 5:54:34 AM

Thanks for sharing this great information, Really looking forward to read more.

totosafedbcom - Wednesday, March 20, 2024 1:06:16 AM

keep posting and updating information.

온라인카지노 - Friday, March 22, 2024 1:24:04 AM

Each of your solutions are acceptable and also strongly practical. My buddies will also feel fortuitous to read this post.

바카라사이트 - Friday, March 22, 2024 1:28:06 AM

I am a new user of this site so here i saw multiple articles and posts posted by this site,

온라인카지노 - Friday, March 22, 2024 1:30:28 AM

Awesome article, it was exceptionally helpful!

온라인카지노 - Friday, March 22, 2024 1:34:13 AM

Excellent information on your blog, thank you for taking the time to share with us.

파워볼게임 - Friday, March 22, 2024 1:37:20 AM

hanks for writing such useful content, I like your style of writing and frequently read your content.

ขาย ปลีก ส่ง น้ำยาบุหรี่ไฟฟ้า - Thursday, April 4, 2024 9:54:26 PM

This blog is so nice to me. I will keep on coming here again and again.

ทางเข้า เล่นหวยยี่กี - Wednesday, April 10, 2024 8:21:17 PM

I appreciate the time and effort you invested in crafting such a thought-provoking piece.

ติดต่อหวย huay bee - Tuesday, April 16, 2024 12:54:41 AM

Computers for Research and Analysis open up vast informational resources for students to explore.

Computer analysis and research - Sunday, April 28, 2024 9:53:38 PM

Thank you for provide us useful information. I've already bookmarked webpage for the future updates.

ultra high purity gas delivery systems - Tuesday, May 7, 2024 5:42:20 AM

Our math games are fun and educational for all players.

cool math games - Saturday, May 11, 2024 3:32:20 PM

Thanks for this post. Make more educational post like this.

red ball 4 - Monday, May 20, 2024 9:34:50 AM

You should know that Your article is an inspiration to many people. gain more knowledge from what you write

สมัคร ag gaming - Tuesday, May 21, 2024 8:04:21 PM

Get top-notch Unit 1 Health and Social Care Assignment Help. Expert guidance for health and social care level 4 and 5, NVQ levels 4 and 5. Contact us now!

HND Assignment Help - Monday, May 27, 2024 11:26:21 PM

Your insights were incredibly engaging and informative. I learned a lot and truly appreciate your effort and expertise.

bad time simulator - Wednesday, May 29, 2024 7:01:07 AM

This was one of the things I really wanted.Thank you so much for sharing.

คาสิโนออนไลน์ - Thursday, May 30, 2024 2:49:30 AM

Usually I never comment on blogs but your article is so convincing that I never stop myself to say something about it.

789 สล็อต - Friday, May 31, 2024 1:59:13 AM

that’s very good article and i like it very very much

ทางเข้า 123bet - Tuesday, June 4, 2024 9:09:09 PM

I am happy I observed this website on Google. Not just content, in fact, the whole site is fantastic

합법 카지노 사이트 - Friday, June 7, 2024 1:06:45 AM

There is definately a lot to find out about this subject. I like all the points you made.

ร้านล้างรถ อุบล - Thursday, June 13, 2024 11:44:37 PM

This is one of the best articles I have ever read. I want you to know.

ทางเข้า sa gaming - Monday, June 17, 2024 4:25:55 PM

Great information on your blog. Thank you for sharing with us. It's nice to find this website.

123bet แนะนำเพื่อน - Tuesday, June 18, 2024 9:46:33 PM

Thanks for sharing this article to us. I gathered more useful information from your blog. Keep sharing more related blogs.

casinositesafe.com/ - Sunday, June 30, 2024 1:13:17 AM

I appreciate your hard work and you have more information. It's very useful.

เกมสล็อต - Sunday, June 30, 2024 9:10:29 AM

i am really impressed with this article.

카지노사이트 - Monday, July 1, 2024 12:41:57 AM

Each one of these small factors are made by utilizing quantity of basis attention.

토토사이트 - Monday, July 1, 2024 12:44:08 AM

Thanks for posting it. I have read your article, it is very informative and helpful for me.I admire the valuable information you offer in your articles.

789betting กีฬา - Monday, July 1, 2024 12:59:31 AM

Your article is a shining example of the power of well-crafted writing.

trang cá cược bóng đá uy tín - Friday, July 5, 2024 11:14:18 PM

Very descriptive post, I loved that bit. Will there be a part 2?

토토사이트 꽁머니 - Wednesday, July 10, 2024 5:49:13 AM

Great Article it its really informative and innovative keep us posted with new updates. its was really valuable. thanks a lot.

เดิมพันกีฬาออนไลน์ - Sunday, July 14, 2024 10:44:50 PM

Thanks for sharing this useful article.

바카라사이트 - Monday, July 22, 2024 2:58:28 AM

Your website deserves all of the positive feedback it’s been getting.

슬롯사이트 - Monday, July 22, 2024 3:00:52 AM

Your article has proved your hard work and experience you have got in this field

토토사이트 - Monday, July 22, 2024 3:02:34 AM

i am really impressed with this article.

카지노사이트 - Monday, July 22, 2024 3:05:16 AM

This site exactly what I was looking for.

홀짝게임 - Monday, July 22, 2024 3:06:33 AM

It is incredibly a comprehensive and helpful blog.

홀짝게임 - Monday, July 22, 2024 3:07:18 AM

It is worth reading for everyone.

안전놀이터 - Monday, July 22, 2024 3:08:03 AM

Your post is so useful to your readers. Keep us updated!

asphalt driveway indianapolis - Tuesday, July 30, 2024 8:52:53 PM

Guide a quartet of animated blobs to create beautiful operatic music in Blob Opera. Adjust their pitch and volume to produce harmonious melodies. This game encourages creativity and offers a fun and engaging experience for music lovers.

blob opera - Tuesday, July 30, 2024 11:59:07 PM

Your blog post was a pleasure to read.

바카라사이트 - Friday, August 2, 2024 1:49:16 AM

Each one of these small factors are made by utilizing quantity of basis attention.

슬롯사이트 - Friday, August 2, 2024 1:54:15 AM

It’s similarly a fantastic write-up i usually certainly appreciated analyzing.

토토사이트 - Friday, August 2, 2024 1:55:50 AM

I definitely enjoying every little bit of it I have you bookmarked to check out new stuff you post

카지노사이트 - Friday, August 2, 2024 1:57:52 AM

This method is actually aesthetically truly the most suitable.

홀짝게임 - Friday, August 2, 2024 1:59:40 AM

It’s a wonderful platform for personal growth.

홀짝게임 - Friday, August 2, 2024 2:01:19 AM

Great article Lot’s of information to Read

안전놀이터 - Friday, August 2, 2024 2:03:09 AM

thats okey?

Slope - Monday, August 12, 2024 6:42:13 AM

Thank you for the information regarding coding, I read it and it is easy to understand and will be useful.

หวย ยี่ กี 5 นาที - Monday, August 12, 2024 10:08:59 AM

MK لباس مردانه is a manufacturer of پیراهن مردانه , پلیور مردانه, شلوار مردانه, men's linen pants, men's shoes, single coats and all kinds of accessories in Iran. MK brand is always trying to bring attractiveness along with quality. With its stunning quality, MK men's clothing will accompany you for many years so that you can always shine in the sweetest moments with a different and beautiful style and leave behind the most beautiful cover. Right now, you can buy all the men's clothing you need to create a beautiful and different style from the MK online store with incredible discounts.

لباس مردانه - Monday, August 26, 2024 2:53:44 AM

It is incredibly a comprehensive and helpful blog.

동행복권파워볼 - Saturday, August 31, 2024 2:04:09 AM

It is worth reading for everyone.

동행복권파워볼 - Saturday, August 31, 2024 2:06:08 AM

Your blog post was a pleasure to read.

메이저놀이터 - Saturday, August 31, 2024 2:07:47 AM

Thanks for the great article today. I like to receive new news all the time.

ดาวน์โหลด bet game - Wednesday, September 4, 2024 9:12:21 PM

It is incredibly a comprehensive and helpful blog.

홀짝게임 - Monday, September 9, 2024 3:39:27 AM

PGPLAY999 รวมจบครบทุกการเดิมพัน
ยุคที่ธุรกิจออนไลน์เติบโตอย่างรวดเร็ว PGPLAY999 ชื่อชื่อที่เข้ามาโดยตรงส่วนใหญ่จะรวมทุกคำขอของนักพนันในที่เดียว PGPLAY999 ไม่เพียงแต่เป็นเว็บออนไลน์ที่เปิดเผยทั่วไปเป็นแพลตฟอร์มที่ไม่จำเป็นสำหรับทุกๆ รูป เหตุผลที่ทำให้ PGPLAY999 โดดเด่นและโดดเด่นในตลาด

PGPLAY999 - Friday, September 13, 2024 7:13:38 PM

We hope you will share some more information about it. We really enjoy your blog & content.

ลาว กาชาด - Tuesday, September 17, 2024 1:48:53 AM

I would like to thank you for allowing us to read and learn here. I really like it.

123bet สล็อต - Tuesday, September 24, 2024 9:27:59 PM

Thank you

globesimregistration.com.ph - Friday, October 4, 2024 3:53:59 AM

I want to tell you that I am really amazed by all your articles. It has knowledge and interesting details

แทงหวย ธ ก ส - Friday, October 4, 2024 4:27:06 PM

It’s a wonderful platform for personal growth.

무료 토토사이트 - Sunday, October 6, 2024 2:34:33 AM

Great article Lot’s of information to Read

엔트리 파워사다리 - Sunday, October 6, 2024 2:36:24 AM

I gotta most loved this site it appears to be exceptionally useful.

카지노사이트 - Sunday, October 6, 2024 2:38:25 AM

Much like how the monoidal identity acts within a category, Telegram provides a central hub of communication. Its efficiency in handling data mirrors the natural transformation of functors between categories, preserving the essential structure of communication."

Telegram - Thursday, October 10, 2024 12:00:07 AM

Telegram operates like the ⊛ operator in a monoidal category, where it brings together different components (users, media, channels) in a coherent and natural way, much like a functor that maintains the integrity of operations between systems."

Telegram ios - Thursday, October 10, 2024 12:01:53 AM

I am so glad that you shared this useful information with us.

คาสิโนออนไลน์ - Friday, October 11, 2024 7:26:41 PM

ท้าให้ลอง สล็อตแตกง่าย เครดิตฟรีหน้าเว็บ เกมดี สนุกมาก ค่ายเกมฮิตอยู่ในนี้ เว็บเดียวจบ ทดลองเล่นฟรี มีโปรโมชั่นมากมาย กับสล็อตออนไลน์ แจกฟรีสปิน ลองแล้วจะติดใจ

jili slot เว็บตรง - Saturday, October 26, 2024 2:02:28 AM

JILI SLOT เพอร์เฟคคอมโบ! เกมลื่นไม่สะดุดไม่กั๊กโบนัสแจ๊กพอตเล่นได้ตลอดทั้งวันเล่นยังไงก็แตกแจกไม่อั้นเว็บตรงไม่ผ่านเอเย่นต์ปลอดภัยมากที่สุด

JILI SLOT - Monday, November 4, 2024 5:11:10 PM

رنگ خوراکی ژله ای

caketasviri - Wednesday, November 6, 2024 7:34:47 AM

This is really a very informative article. but full of substance I like it you write well

ลิงค์รับทรัพย์ bg casino - Friday, November 8, 2024 8:09:28 PM

تقدم شركة كايرو هايتس مجموعة من أكبر المشروعات السكنية المتميزة وشقق للبيع بالقاهرة الجديدة والتجمع الخامس والعديد من الوحدات السكنية الراقية بعقارات بيت الوطن والتى تتميز بالخصوصية والهدوء والإطلالة الفريدة على حدائق ومساحات خضراء.
تختار كايرو هايتس بالقاهرة الجديدة مشروعاتها بعناية وبمواقع استراتيجية بحيث تكون قريبة من مناطق الخدمات والمراكز الترفيهية وأشهر النوادى والمؤسسات التعليمية الهامة.

saged - Tuesday, November 12, 2024 10:45:13 PM

I admire your ability to distill complex ideas into clear and concise prose.

หวย มาเล ย์ วัน นี้ 4d - Tuesday, November 12, 2024 10:51:23 PM

Určite skús SynotTip alebo Tipsport Casino. Sú to české značky s dlhou tradíciou, kde sa nemusíš báť o bezpečnosť. Slovenských hráčov berú úplne v pohode, stačí si len overiť účet. Bonusy? Napríklad SynotTip ti dáva free spiny bez vkladu na začiatok, čo je super na zoznámenie sa s platformou. Tipsport má zas fajn vstupný bonus na prvý vklad, takže ak plánuješ hrať za viac, oplatí sa tam zaregistrovať. Ak máš rád jackpoty, tak tieto kasína ich ponúkajú dosť často a nie sú len pre veľkých hráčov.

AnnaSokolski - Saturday, November 23, 2024 9:14:46 AM

Telegram provides an excellent platform for Hong Kong-based developers to discuss complex topics like Category Theory in programming. The article’s exploration of monoidal functors and applicative functors in C# is an advanced topic, and joining Telegram groups dedicated to functional programming or mathematics in programming can help Hong Kong developers deepen their understanding and collaborate with like-minded professionals.

Telegram下载 - Wednesday, November 27, 2024 1:47:08 AM

Understanding abstract concepts like monoidal functors and applicative functors can be challenging, but Telegram makes it easier to break down complex topics and share resources. By connecting with other C# developers or category theory enthusiasts in Hong Kong, one can access tutorials, explanations, and coding examples that build a practical understanding of these functional programming concepts.

Telegram中文语言包 - Wednesday, November 27, 2024 1:48:16 AM

Telegram can serve as a valuable resource for Hong Kong software engineers who want to dive into Category Theory and its application in C#. The article on monoidal functors and applicative functors is just the tip of the iceberg in functional programming. Joining Telegram channels related to advanced C# and functional programming can help keep developers updated with new trends and offer an avenue for solving programming challenges collectively.

Telegram中文版 - Wednesday, November 27, 2024 1:49:16 AM

Your comments make this discussion richer.

91 Club Free Gift Code Generator APK - Wednesday, December 4, 2024 10:36:39 PM

Hello, I am an online gambler and would like to recommend a good, reliable website. Really pay every withdrawal amount. Plus a stable game system No lag, no freezes. Good quality website, high security, no cheating, definitely no user lock. If interested, come and try playing. New members receive double profits.
betflik : http://betflik45.club

betflik - Friday, December 6, 2024 12:04:46 AM

We provide support for those looking for 'Take my GED for me' or 'Take my TEAS exam' solutions. Need help with your GED or TEAS exam? We offer services so you can pay someone to take your GED or TEAS exam, hire someone for exam assistance and solutions.

Hire someone To Take My GED exam - 1 hour ago

Are you looking for who will 'Write My Dissertation For Me?' We provide support for those looking for 'Dissertaion Writing Services' or 'Dissertation Help'. We offer services so you can 'Pay Someone To Do Your Dissertation'.-

Write My Dissertation For Me - 1 hour ago

Seeking a reliable local SEO company in Berkshire for SEO optimization, online marketing, website design, Google Ads management, Social Media, USA, UK, Australia, UAE.

SEO Berkshire - 1 hour ago

Dixin's Blog