Quantum computing and topological qubits explained clearly
Don't let yourself be intimidated by all the quantum jargon. The bases of quantum computing are not that complicated, and I can explain them to anyone who understands programming, classical logic gates, the bare minimum about complex numbers and linear algebra… I'll do so in the light of Microsoft's recent announcement of a new discovery that could bring us much more stable quantum computers.
But first, a disclaimer: I do work at Microsoft, but I don't work on the quantum computing team. I'm just an enthusiast developer who happens to be trained in quantum mechanics.
What did Microsoft just announce?
Microsoft's quantum computing group announced in Nature they had observed “quantized Majorana conductance”. Unless you're well-versed in quantum mechanics, I don't recommend you check it out, as even the abstract is quite technical. Let me explain what it's essentially saying.
There's a type of particle called a “Majorana fermion” (after Ettore Majorana, who predicted their existence in 1937) that is its own anti-particle. Don't worry if you don't know exactly what that entails, that's not the important part. What's important is that specially prepared pairs of these particles can exhibit a very interesting property: it is possible to entangle the states of those particles, in the same way that you'd braid two pieces of string together.
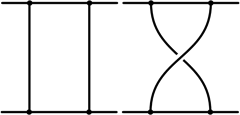
Imagine two rubber bands attached at both of their ends to some common support that cannot move. The bands may for example be parallel to each other. That's one state. Now exchange one of the extremities of each rubber band. That's another state. Notice that even though the rubber bands can be deformed, there is no way to go from one state to the other, except by detaching the extremities and reattaching them. The bands will continue to have, in one case an even numbers of overlaps, and in the other an odd number of overlaps. This sort of property that can resist continuous deformation of the system is the subject of a branch of mathematics called topology (of which a whole sub branch is the study of braids). Pairs of Majorana fermions, if properly prepared, can exhibit such properties.
Majorana fermions were theoretical until recent years. We think neutrinos (a very elusive type of particle involved in radioactivity) may be Majorana fermions, but we're not sure yet. Last Summer, the first smoking gun of quasi-particles behaving like Majorana fermions has been announced by a group of scientists from Stanford. Quasi-particles are configurations of quantum fields in a material that behave like elementary particles, but aren't. They are typically found in two-dimensional materials like the contact surface between two materials, or single-dimensional materials like a wire.
What the Microsoft quantum computing group announced this first week of April 2018 is that they have strong and consistent evidence for the presence of Majorana quasi-particles in nanowires. In simpler words, they have a device with the elusive Majoranas in it.
Why is it important?
Being immune to deformations is a very interesting property if you want to build a quantum computer. Quantum states tend to be confined to small scales and low temperatures, because interaction with large and warm systems will destroy them. Even a small perturbation from the environment can have catastrophic effects on the “quantumness” of the system, which is precisely what we're interested in with quantum computing. You can deal with it in a few ways: you can keep the system small (but that limits how much you can achieve), you can add redundancy to the system (but that makes it more difficult to scale the system up), or you can find more stable quantum systems (that's the direction the Microsoft team has chosen to take).
Topological quantum states can still be destroyed by the environment, but there are ways to mitigate the problem that other sorts of quantum states don't have access to. Typically, the only thing that can destroy a topologically entangled pair of Majoranas, is the interaction with another pair in a state that can collide with it. This does happen, because in quantum mechanics, such pairs spontaneously pop into existence all the time. You can make that very unlikely however, with a simple trick: move both halves of the pair apart as much as you can. The particles will remain entangled (so their state remains unchanged), but for another pair to be able to destroy the state, it would have to be similarly stretched across space. This is considerably less likely than if the pair was spatially close together.
The Microsoft results, the implementation of Majorana states, are a very important step on the path of stable, reliable, and scalable quantum computing. This is why it matters.
But let's take a step back, and try to understand what quantum computing is, and why we want it.
A quick intro to quantum mechanics
I should probably stress out before I go any further that while I'll teach you rudiments of quantum mechanics, this is not going to give you a deep understanding of it. It will however give you an understanding of the mechanisms at work in quantum computing. In other words, you won't necessarily understand Schrödinger's cat much better, but you'll be able to understand and use basic quantum algorithms.
Quantum states
In any text about quantum mechanics, you'll read a lot about “quantum states”. I've already used the term a lot in this post without properly defining it. A state is the condition a system is in. For example, a bit can have one of two states: 0 and 1. A byte's state can be any integer between 0 and 255. You could also say that a byte's state is described by the states of each of its eight constituent bits. Now that's interesting, because those eight bits can be seen as independent sub-states. They are orthogonal. You could describe a byte as a point in an eight-dimensional space where each dimension is one of the bits, and where the coordinates can be 0 or 1. When you think about it, any classical physical system can be described with a set of coordinates over elementary, orthogonal states.
For example, the state of a ball may be described by its position (three coordinates), and its velocity (three coordinates again).
Quantum states are pretty much the same, with an interesting twist… A quantum state is also described with a set of coordinates, but in a more abstract space than what we've considered so far, and with complex coordinates.
Now hold it right there… Complex numbers? Why? How can complex numbers appear in nature? I can only see real numbers around. Well, in our classical perception of the world, yes, only real numbers ever show up. If you measure the width of your desk, you will never, ever measure meters. In the quantum world, however, complex numbers are the norm. Complex numbers are also, in many ways, easier to manipulate and more “natural” than real numbers. All second degree complex equations have solutions, for instance, whereas real ones don't ( for example).
A good way to think about complex numbers in physics is to imagine them as a real amplitude with a phase, rather than a combination of real and imaginary parts. The phase is an angle between 0 and (360° in radians). Positive numbers have a 0 phase, negative numbers have a phase, i has a phase, and all other values are possible. When you multiply two numbers, the amplitudes get multiplied, and the phases get added (modulo ). When you add two numbers, you can imagine them as being drawn one at the end of the other.
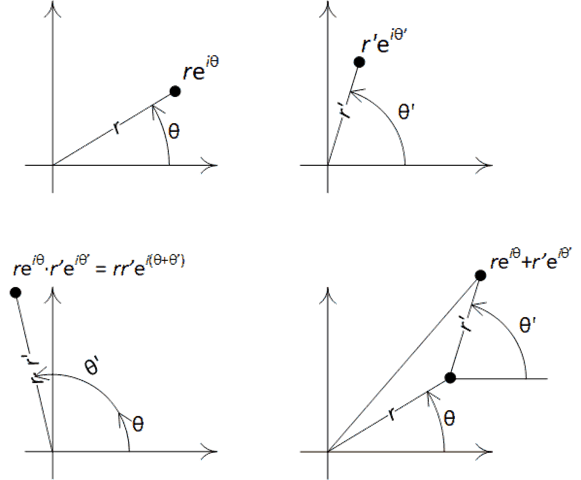
Depending on how the phases align or not, adding complex numbers may result in constructive or destructive interference.

This ability for out of phase states to interfere, much like waves do, is key to quantum weirdness. Let's look at the specifics.
Let's get back to our classical bit and try to understand what would be a quantum equivalent, a “qubit”. To build this, we start from two orthogonal states (that's the first difference with the classical bit where 0 and 1 are not orthogonal). We'll arbitrarily label these states and . This is just a weird physicist's notation, labelling two states. There is no numerical value associated with them, they are just equivalents of the zero and one states of a classical bit.
The state of the qubit can be described by complex coordinates along those two orthogonal states:
So far, we've just thrown some definitions, without explaining where they're coming from, what they represent, or what they mean. and may be any possible pair of orthogonal values that we may measure for the same quantity. For example, they may represent the spin of an electron being up or down, or they may be the untangled and tangled states of the braid we were talking about earlier. The calculations will be the same no matter what the physical substrate actually is. This is good: we wouldn't want our Q# code to have to look different whether we run it on a Google qubit, or on a Microsoft Majorana topological qubit.
Our qubit already is a superset of a classical bit: {a: 1, b: 0} and {a: 0, b: 1} correspond to classical bit values 0 and 1. We do have however other possible states: other complex values for a and b, which physicists call superpositions. There is just one constraint on these coordinates, and to understand it, we'll introduce some physical meaning with what happens when we measure a quantum state.
Measurement
In order to extract information from the system, we need to measure it. Measuring has the effect of collapsing the state of the system along one, and one only, of the possible classical states, and . The probability of getting one or the other is the square of the amplitude of the state's component along it (if the states are normalized, more on this in a second). Applying this to the two base states, we can see that for , the probability of measuring is 1, and the probability of measuring is zero. For , those are reversed. We thus get confirmation that those two states are measured as themselves. They are classical states, and have no uncertainty associated with them.
Now let's look at a state that is a superposition of both states, the state above. The probability to get is , and the probability to get is . No other result is possible, which means that the sum of those probabilities should be 1. The probabilities of a complete set of possible outcomes always sum up to 1. Numerically, this translates as . This is what we mean by “normalized state”, and it is a constraint that we'll enforce to keep the formulas simple: not enforcing it would add a scale factor to the probability formula. Not a big deal, but it's fine to see it as a useful convention.
Can you guess what the probabilities will be to measure either value from a qubit built as a superposition of equal amounts of each state?
The squared amplitude for each value is the same: . This means that, as expected, each value is equally likely, and that the probabilities add up to 1.
Once a state has been measured, its state becomes whichever base state happens to have been randomly selected. It is no longer a superposition. So in the previous example, a measure will give one or the other value half the time. Let's say we measured . The state is now , so if we measure it again, because it is now this state, and we've seen measured as 100% of the time, we will always measure .

We now have the basic understanding of a qubit, and of what happens when we attempt to measure it. Let's now look at what operations we can perform on qubits, in which we'll introduce the quantum building blocks that are analogous to classical logic gates.
Quantum operators
It is possible to transform quantum states while keeping their quantum properties (unlike what happens when measuring them). Those transformations must obey a number of rules in order to be valid, and one of those rules is that the transformed state must still be a valid quantum state, for which the probabilities of observing the various possible states have a sum of 1. Such transformations are called “unitary”, and they can be described with matrices. Applying the transformation is the same thing as multiplying the matrix by the vector representing the state.
Let's start with one of the simplest operations we can do: NOT. A NOT gate, both in classical and quantum computing, transforms 0 into 1, and 1 into 0. The matrix for this is easy to build:
It's easy to see that this works as expected:
A NOT gate is usually represented with the following symbol:

Another interesting gate is the Hadamard gate, or H gate:

This gate transforms into , and into . This is interesting because if you started with one of the base states, you can use this to transform it into a superposition.
Let's move on to gates that involve more than one qubit. Things are going to get a lot more exciting and spooky, because this will open the door to quantum entanglement.
To represent two qubits, we just use a tensor product. The individual base states for our dual-qubit quantum states are all tensor products of the base states of both qubits. There's 4 of them, that we'll use as the bases for the space of 2-qubit states:
Extrapolating from this, you should start to see how this will will scale: a 8 qubit system will be represented by vectors in a space whose base are the tensor products of eight individual states, each of which have two base states. That's a dimensional space. As you can see, the number of degrees of freedom of the system literally grows exponentially with the number of qubits, and yet, the number of gates you need to process them grows only linearly. That is what makes quantum computers more powerful (for algorithms that can take advantage of them) than classical ones. I cannot stress enough that this is one case where the word “exponential” is actually justified, because it is so rarely the case. It also shows how the benefits of quantum computing are ones of scalability: it can solve problems where the complexity grows too fast for classical computers, by growing the computing power non-linearly.
If we build a state from two qubits
and
That same state can be represented in terms of tensor products as:
Remember however that any linear combination of the four base states is possible. Is it always possible to express such a state as the tensor product of two qubits? In other words, given a state , is it always possible to find , , , and such that:
The answer is no. For example, cannot be expressed as a tensor product of states of individual qubits. It's easy to see that since , or would have to be zero, but that would make zero, which is false.
Such a state, that can be realized in a two-qubit system, but isn't a simple combination of two qubits, is called an entangled state. This name is justified by an interesting property, which is that the measurement of the two bits is tightly coupled.
In the example above (known as a Bell state), the two states that can be measured are and . All other states have a zero probability of coming up. Another way to say this is that if the first bit is measured as a 1, the second bit will also be measured as a 1, and the same goes for measuring a zero. There is still chance involved in the measurement, but the system's bits are strangely coupled. It looks like the first bit is communicating its own measure to the second one, instantly (and even potentially, over huge distances that couldn't be covered by a physical signal that would have to be faster than light, which is impossible).
From a quantum perspective, nothing really weird is going on: there is only one state, that spans what we as classical observers identify as two separate entities. There is only one measurement being performed, over a single system, even if that system is delocalized. When we choose to measure the individual classical bits, we're slicing into that state in "diagonal", we're looking at the physical system from a point of view that isn't particularly natural. The weirdness is in our perspective.
There's more to quantum entanglement (for instance it's what enables quantum teleportation), but you should know enough from that brief introduction to understand its usefulness in the context of quantum computing. Entangled states are those states that cannot be described as the combination of its qubits. They highlight those cases where the system is more than the sum of its parts.
Another consequence of the existence of entangled states is that you can't take shortcuts when simulating qubits on classical hardware: you need to consider the whole exponentially growing set of base states, and can't consider the qubits in isolation. This means that the simulation will become impractical very fast, as the number of qubits grows.
So how do we build one of those states? For that, we'll need new multiple-qubit gates. The first we need is the controlled NOT gate, or CNOT. With this gate, the first qubit acts as a control (it's unchanged by the operation), and the second bit is inverted only if the first qubit is (otherwise it's left alone):

It's easy to verify that, as announced, we have the following mapping on the base states:
If we first apply a Hadamard gate on the first qubit, then CNOT on the resulting state, the resulting combination has the interesting property that it maps onto the Bell state .
Let's verify this. The Hadamard gate on the first qubit maps onto . Then, the CNOT gate leaves unchanged while it maps onto . QED, the resulting state is , and we have successfully prepared an entangled state. It's left as an exercise to the reader that the other three base states also get mapped to entangled states.
Of course, there are many other possible gates. The point being that like for classical computing, there are minimal universal sets of gates that are enough, when combined, to perform almost any calculations. Also like in classical computing, implementing an algorithm when all you have is the lowest level of gates is not exactly the easiest thing in the world. With classical computers, we have several layers of abstraction that enables us to express computations with high-level languages, but we have no such luxury (yet) with quantum computers. Even something like Q# only enables developers to mix high-level classical constructs with low-level qubit manipulation.
The trouble with quantum computers: the inaccessible state
With this, we've in principle set-up all of the basic concepts needed by quantum computing. It even looks like we have a way to simultaneously perform arbitrary calculations on all possible inputs, in the time it would take a classical computer to run the same calculations on just one input. Prepare a state such that each qubit is a perfect superposition of and , run it through gates that implement your calculation, and presto!, you've got a result that is the superposition of the results for all possible input values. If you had access to that result state, there are simple tricks that would enable you to actually extract each individual result.
That is precisely the issue, though: we do not have access to the quantum state, not directly at least. The quantum state may be the true physical state of the system, but we can never get all the information about it. All we can do is measure it, and as we've seen, measurement is a destructive, stochastic, and lossy process. In effect, it is a general principle that you cannot extract more than bits of information out of qubits. Does this mean that we've just lost all the potential benefits of quantum computing? Not exactly, but it does mean that we'd better make those measurements count...
The simplest win: guess the function
Imagine that we have an unknown function that takes one classical bit as an input, and outputs one classical bit. There are only four such functions:
Two of those ( and ) are constants. If you wanted to determine if the function is one of those two constant functions with a classical computer, you have to perform exactly two operations: feed it a 0, then feed it a 1. If both results are equal, the function is constant.
A quantum computer can do that in only one operation. The trick to do it is to sandwich between two Hadamard gates a special function called an oracle, that is built from the one we're trying to guess. We'll then feed a into the process. The oracle to use is the following:
Whether the result of the evaluation of is 0 or 1, if the function is constant, the same phase will be applied to both of the base states. This means that any quantum state will come out unchanged, except for the occasional phase. And remember from what we said about measurement that phase cannot change the probability of the outcomes, only the amplitudes count.
Now if the function is not constant, each of the base states will get opposite phase shifts. All we have to do now is add the Hadamard gates around the oracle, and feed the system the state.
Let's break the whole process down from beginning to end. The first Hadamard gate will change the state into a superposition of the base states. If the function is constant, the oracle will give back the same state, with maybe a phase change. The second Hadamard gate will transform that back into , with maybe a phase change. If the function is not constant, a different state comes out, with a phase shift on one of the base states, and not on the other. In this case, the second Hadamard gate is going to transform that into a pure . All we have to do is measure the output. If the function is constant, we'll get 100% of the time, and if it's not, we'll get 100% of the time. We have successfully obtained information from the system, without any quantum uncertainty, faster than a classical system ever could.
Conclusion
We went through one of the simplest examples of a quantum algorithm that outperforms any possible classical system. The principles we've applied are the same you'd apply at a larger scale, but the benefits would then be considerably more substantial. We take a known base state, change it into some superposed quantum state, then apply some transformation, and come back to pure base states that depend on the outcome of the computation, then we measure. We will not gain the exponentially faster parallel computing we may have been led to hope for from the behavior of the quantum state and gates, but we do get very real benefits on appropriate processes. Learning and discovering those processes can be a lot more complicated than what I've shown in this article, but I hope that you've gained an understanding and an appreciation of it. Most of all, I hope things look a little less mysterious, and a lot more fascinating, that you'll be driven to read more about quantum computing. Tell me what you think in the comments, what you'd like to read in future posts, and of course, let me know if I got anything wrong.