Category Theory via C# (4) Functor And IEnumerable<>

Wednesday, December 5, 2018

[LINQ via C# series]

[Category Theory via C# series]

Latest version: https://weblogs.asp.net/dixin/category-theory-via-csharp-3-functor-and-linq-to-functors

Functor and functor laws

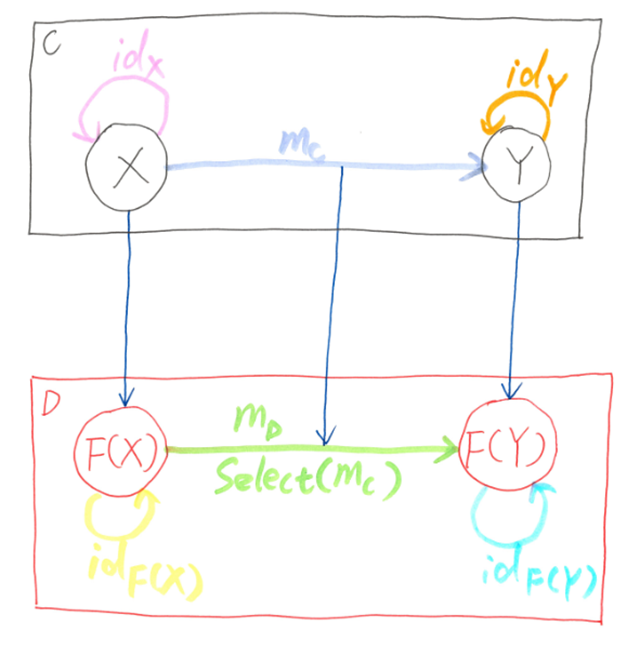
A functor F: C → D is a structure-preserving mapping from category C to category D:

As above diagram represented, F:

maps objects X, Y ∈ ob(C) to objects F(X), F(Y) ∈ ob(D)
also maps morphism m_C: X → Y ∈ hom(C) to a new morphism m_D: F(X) → F(Y) ∈ hom(D)
- To align to C#/.NET terms, this mapping ability of functor will be called “select” instead of “map”. That is, F selects m_C to m_D .

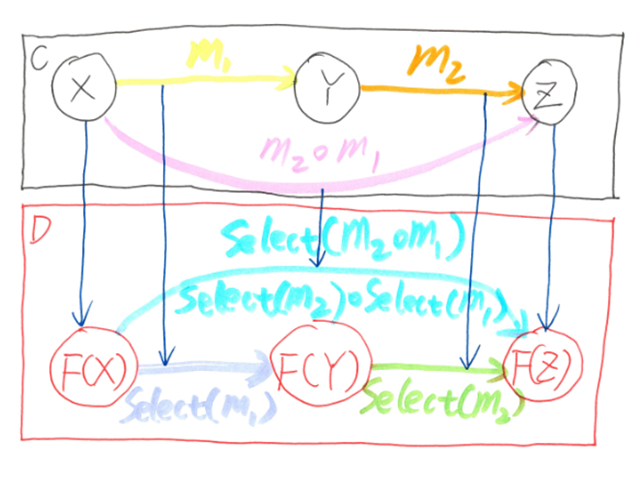
and satisfies the functor laws:

F(id_X) ≌ id_F(X), see above image
Select(m₂ ∘ m₁) ≌ Select(m₂) ∘ Select(m₁)

So the general functor should be like:

// Cannot be compiled.
public interface IFunctor<in TSourceCategory, out TTargetCategory, TFunctor<>>
    where TSourceCategory : ICategory<TSourceCategory>
    where TTargetCategory : ICategory<TTargetCategory>
    where TFunctor<> : IFunctor<TSourceCategory, TTargetCategory, TFunctor<>>
{
    IMorphism<TFunctor<TSource>, TFunctor<TResult>, TTargetCategory> Select<TSource, TResult>(
        IMorphism<TSource, TResult, TSourceCategory> selector);
}

A TFunctor<>, which implements IFunctor<…> interface, should have a method Select, which takes a morphism from TSource to TResult in TFromCategory, and returns a morphism from TFunctor<TSource> to TFunctor<TResult> in TToCategory.

C#/.NET functors

A C# functor can select (maps) a morphism in DotNet category to another morphism still in DotNet category, such functor maps from a category to itself is called endofunctor.

Endofunctor

A endofunctor can be defined as:

// Cannot be compiled.
public interface IEndofunctor<TCategory, TEndofunctor<>>
    : IFunctor<TCategory, TCategory, TEndofunctor<>>
    where TCategory : ICategory<TCategory>
    where TEndofunctor<> : IFunctor<TEndofunctor, TEndofunctor<>>
{
    IMorphism<TEndofunctor<TSource>, TEndofunctor<TResult>, TCategory> Select<TSource, TResult>(
        IMorphism<TSource, TResult, TCategory> selector);
}

So an endofunctor in DotNet category, e.g. EnumerableFunctor<T>, should be implemented as:

// Cannot be compiled.
// EnumerableFunctor<>: DotNet -> DotNet 
public class EnumerableFunctor<T> : IFunctor<DotNet, DotNet, EnumerableFunctor<>>
{
    public IMorphism<EnumerableFunctor<TSource>, EnumerableFunctor<TResult>, DotNet> Select<TSource, TResult>(
        IMorphism<TSource, TResult, DotNet> selector)
    {
        // ...
    }
}

Unfortunately, all the above code cannot be compiled, because C# does not support higher-kinded polymorphism. This is actually the biggest challenge of explaining category theory in C#.

Kind issue of C# language/CLR

Kind is the (meta) type of a type. In another word, a type’s kind is like a function’s type. For example:

int’s kind is *, where * can be read as a concrete type or closed type. This is like function (() => 0)’s type is Func<int>.
IEnumerable<int> is a closed type, its kind is also *.
IEnumerable<> is a open type, its kind is * → *, which can be read as taking a closed type (e.g. int) and constructs another closed type (IEnumerable<int>). This is like function ((int x) => x)’s type is Func<int, int>.
In above IFunctor<TFromCategory, TToCategory, TFunctor<>> definition, its type parameter TFunctor<> has a kind * → *, which makes IFunctor<TFromCategory, TToCategory, TFunctor<>> having a higher order kind: * → * → (* → *) → *. This is like a function become a higher order function if its parameter is a function.

Unfortunately, C# does not support type with higher order kind. As Erik Meijer mentioned in this video, the reasons are:

CLR does not support higher order kind
Supporting higher order kind causes more kind issues. For example, IDictionary<,> is a IEnumerble<>, but they have different kinds: * → * → * vs. * → *.

So, instead of higher-kinded polymorphism, C# recognizes the functor pattern of each functor, which will be demonstrated by following code.

The built-in IEnumerable<> functor

IEnumerable<T> is the a built-in functor in C#/.NET. Why it is a functor and How is this implemented? First, in DotNet category, if IEnumerable<> is a functor, it should be an endofunctor IEnumerable<>: DotNet → DotNet.

public static IMorphism<IEnumerable<TSource>, IEnumerable<TResult>, DotNet> Select<TSource, TResult>(
    IMorphism<TSource, TResult, DotNet> selector)
{
    // ...
}

IEnumerable<T> should be able to do the above select/map from DotNet category to DotNet category.

Second, in DotNet category, morphisms are functions. That is, IMorphism<TSouece, TResult, DotNet> and Func<TSouece, TResult> can convert to each other. So above select/map is equivalent to:

// Select = selector -> (source => result)
public static Func<IEnumerable<TSource>, IEnumerable<TResult>> Select<TSource, TResult>(
    Func<TSource, TResult> selector)
{
    // ...
}

Now Select’s type is Func<T1, Func<T2, TResult>>, so it is a curried function. It can be uncurried to a equivalent Func<T1, T2, TResult>:

// Select = (selector, source) -> result
public static IEnumerable<TResult> Select<TSource, TResult>( // Uncurried
    Func<TSource, TResult> selector, IEnumerable<TSource> source)
{
    // ...
}

The positions of 2 parameters can be swapped:

// Select = (source, selector) -> result
public static IEnumerable<TResult> Select<TSource, TResult>( // Parameter swapped
    IEnumerable<TSource> source, Func<TSource, TResult> selector)
{
    // ...
}

The final step is to make Select an extension method by adding a this keyword:

// Select = (this source, selector) -> result
public static IEnumerable<TResult> Select<TSource, TResult>( // Extension method
    this IEnumerable<TSource> source, Func<TSource, TResult> selector)
{
    // ...
}

which is just a syntactic sugar and does not change anything. The above transformation shows:

In DotNet category, IEnumerable<>’s functoriality is equivalent to a simple familiar extension method Select
If the last Select version above can be implemented, then IEnumerable<T> is a functor.

IEnumerable<T>’s Select extension method is already implemented as System.Linq.Enumerable.Select. But it is easy to implement manually:

[Pure]
public static partial class EnumerableExtensions
{
    // C# specific functor pattern.
    public static IEnumerable<TResult> Select<TSource, TResult>( // Extension
        this IEnumerable<TSource> source, Func<TSource, TResult> selector)
    {
        foreach (TSource item in source)
        {
            yield return selector(item);
        }
    }

    // General abstract functor definition of IEnumerable<>: DotNet -> DotNet.
    public static IMorphism<IEnumerable<TSource>, IEnumerable<TResult>, DotNet> Select<TSource, TResult>
        (this IMorphism<TSource, TResult, DotNet> selector) => 
            new DotNetMorphism<IEnumerable<TSource>, IEnumerable<TResult>>(
                source => source.Select(selector.Invoke));
}

So IEnumerable<T> is a functor, The both Select functions are implemented as extension method for convenience.

Functor pattern of LINQ

Generally in C#, if a type F<TSource>:

have a instance method or extension method Select, taking a Func<TSource, TResult> parameter and returning a F<TResult>

then:

F<> is an endofunctor F<>: DotNet → DotNet
- F<> maps objects TSource, TResult ∈ ob(DotNet) to objects F<TSource>, F<TResult> ∈ ob(DotNet)
- F<> also selects morphism selector : TSource → TResult ∈ hom(DotNet) to new morphism : F<TSource> → F<TResult> ∈ hom(DotNet)
F<> is a C# functor, its Select method can be recognized by C# compiler, so the LINQ syntax can be used:

IEnumerable<int> enumerableFunctor = Enumerable.Range(0, 3);
IEnumerable<int> query = from x in enumerableFunctor select x + 1;

which is compiled to:

IEnumerable<int> enumerableFunctor = Enumerable.Range(0, 3);
Func<int, int> addOne = x => x + 1;
IEnumerable<int> query = enumerableFunctor.Select(addOne);

IEnumerable<>, functor laws, and unit tests

To test IEnumerable<> with the functor laws, some helper functions can be created for shorter code:

[Pure]
public static class MorphismExtensions
{
    public static IMorphism<TSource, TResult, DotNet> o<TSource, TMiddle, TResult>(
        this IMorphism<TMiddle, TResult, DotNet> m2, IMorphism<TSource, TMiddle, DotNet> m1)
    {
        Contract.Requires(m2.Category == m1.Category, "m2 and m1 are not in the same category.");

        return m1.Category.o(m2, m1);
    }

    public static IMorphism<TSource, TResult, DotNet> DotNetMorphism<TSource, TResult>
        (this Func<TSource, TResult> function) => new DotNetMorphism<TSource, TResult>(function);
}

The above extension methods are created to use ∘ as infix operator instead of prefix, for fluent coding, and to convert a C# function to a morphism in DotNet category.

And an Id helper function can make code shorter:

[Pure]
public static partial class Functions
{
    // Id is alias of DotNet.Category.Id().Invoke
    public static T Id<T>
        (T value) => DotNet.Category.Id<T>().Invoke(value);
}

Finally, an assertion method for IEnumerable<T>:

// Impure.
public static class EnumerableAssert
{
    public static void AreEqual<T>(IEnumerable<T> expected, IEnumerable<T> actual)
    {
        Assert.IsTrue(expected.SequenceEqual(actual));
    }
}

The following is the tests for IEnumerable<T> as a general functor - selecting/mapping between objects and morphisms:

[TestClass()]
public partial class FunctorTests
{
    [TestMethod()]
    public void EnumerableGeneralTest()
    {
        IEnumerable<int> functor = new int[] { 0, 1, 2 };
        Func<int, int> addOne = x => x + 1;

        // Functor law 1: F.Select(Id) == Id(F)
        EnumerableAssert.AreEqual(functor.Select(Functions.Id), Functions.Id(functor));
        // Functor law 2: F.Select(f2.o(f1)) == F.Select(f1).Select(f2)
        Func<int, string> addTwo = x => (x + 2).ToString(CultureInfo.InvariantCulture);
        IMorphism<int, int, DotNet> addOneMorphism = addOne.DotNetMorphism();
        IMorphism<int, string, DotNet> addTwoMorphism = addTwo.DotNetMorphism();
        EnumerableAssert.AreEqual(
            addTwoMorphism.o(addOneMorphism).Select().Invoke(functor), 
            addTwoMorphism.Select().o(addOneMorphism.Select()).Invoke(functor));
    }
}

And the following is the tests for IEnumerable<T> as a C# functor:

public partial class FunctorTests
{
    [TestMethod()]
    public void EnumerableCSharpTest()
    {
        bool isExecuted1 = false;
        IEnumerable<int> enumerable = new int[] { 0, 1, 2 };
        Func<int, int> f1 = x => { isExecuted1 = true; return x + 1; };

        IEnumerable<int> query1 = from x in enumerable select f1(x);
        Assert.IsFalse(isExecuted1); // Laziness.

        EnumerableAssert.AreEqual(new int[] { 1, 2, 3 }, query1); // Execution.
        Assert.IsTrue(isExecuted1);

        // Functor law 1: F.Select(Id) == Id(F)
        EnumerableAssert.AreEqual(enumerable.Select(Functions.Id), Functions.Id(enumerable));
        // Functor law 2: F.Select(f2.o(f1)) == F.Select(f1).Select(f2)
        Func<int, string> f2 = x => (x + 2).ToString(CultureInfo.InvariantCulture);
        EnumerableAssert.AreEqual(
            enumerable.Select(f2.o(f1)), 
            enumerable.Select(f1).Select(f2));
        // Functor law 2: F.Select(f2.o(f1)) == F.Select(f1).Select(f2)
        EnumerableAssert.AreEqual(
            from x in enumerable select f2.o(f1)(x), 
            from y in (from x in enumerable select f1(x)) select f2(y));
    }
}

IEnumerable<> is like the List functor in Haskell.

https://ma-study.blogspot.com/

medicalphd - Monday, December 13, 2021 12:37:14 PM

Hello ! I am the one who writes posts on these topics majorsite I would like to write an article based on your article. When can I ask for a review?

majorsite - Thursday, October 27, 2022 11:34:48 PM

This method is actually aesthetically truly the most suitable.

온라인카지노사이트 - Sunday, June 23, 2024 2:40:48 AM

It’s a wonderful platform for personal growth.

토토사이트 모음 - Sunday, June 23, 2024 2:42:33 AM

Dixin's Blog