Category Theory via C# (9) Bifunctor
[LINQ via C# series]
[Category Theory via C# series]
Latest version: https://weblogs.asp.net/dixin/category-theory-via-csharp-5-bifunctor
Bifunctor
As discussed in all the previous functor parts, a functor is a wrapper of a object with a “Select” ability to preserve a morphism to another‘
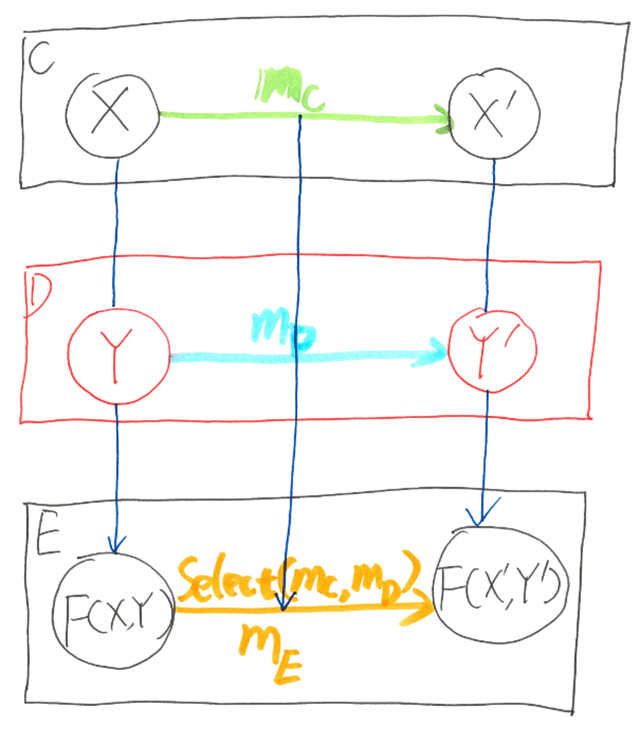
A bifunctor, as the name implies, is a wrapper of 2 objects, with a “Select” ability to preserve 2 morphisms to another morphism:
As above diagram represented, F:
- maps objects X ∈ ob(C), Y ∈ ob(D) to objects F(X, Y) ∈ ob(E)
- also maps morphism mC: X → X’ ∈ hom(C), mD: Y → Y’ ∈ hom(D) to a new morphism mE: F(X, Y) → F(X’, Y’) ∈ hom(E)
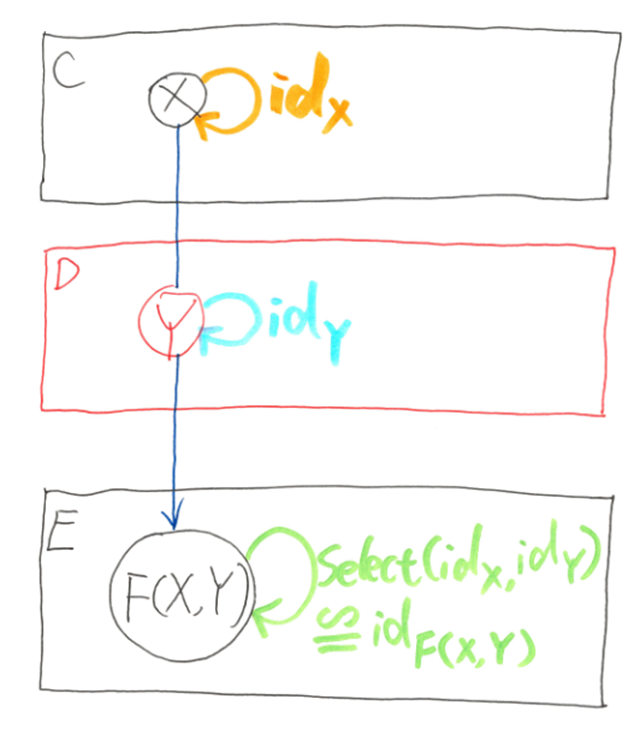
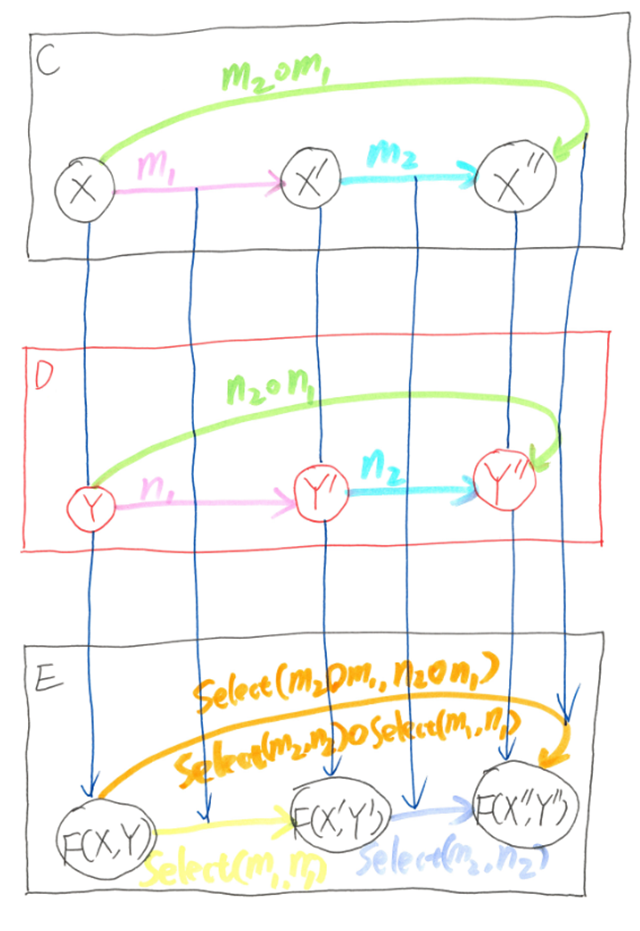
and satisfies the functor laws:
Remember the pseudo C# definition of functor:
// Cannot be compiled. public interface IFunctor<in TSourceCategory, out TTargetCategory, TFunctor<>> where TSourceCategory : ICategory<TSourceCategory> where TTargetCategory : ICategory<TTargetCategory> where TFunctor<> : IFunctor<TSourceCategory, TTargetCategory, TFunctor<>> { IMorphism<TFunctor<TSource>, TFunctor<TResult>, TTargetCategory> Select<TSource, TResult>( IMorphism<TSource, TResult, TSourceCategory> selector); }
Similarly, bifunctor can be defined as:
// Cannot be compiled public interface IBinaryFunctor<in TSourceCategory1, in TSourceCategory2, out TTargetCategory, TBinaryFunctor< , >> where TSourceCategory1 : ICategory<TSourceCategory1> where TSourceCategory2 : ICategory<TSourceCategory2> where TTargetCategory : ICategory<TTargetCategory> where TBinaryFunctor< , > : IBinaryFunctor<TSourceCategory1, TSourceCategory2, TTargetCategory, TBinaryFunctor< , >> { IMorphism<TBinaryFunctor<TSource1, TSource2>, TBinaryFunctor<TResult1, TResult2>, TTargetCategory> Select<TSource1, TSource2, TResult1, TResult2>( IMorphism<TSource1, TResult1, TSourceCategory1> selector1, IMorphism<TSource2, TResult2, TSourceCategory2> selector2); }
As above definition mentioned, bifunctor wraps 2 objects. So here TBinaryFunctor< , > takes 2 parameters so that it can wrap 2 types. Later the Select function will be implemented as extension method for each bifunctor, the same as how functors are handled.
Tri-functor, and multi-functor can be defined and implemented similarly.
C#/.NET bifunctor
Theoretically, the intuitive bifunctor is Tuple< , >. However, as a previous part mentioned, Tuple< , > can have unexpected behavior in C#/LINQ context, so it will only be considered functor-like. So, to be consistent, Tuple<> or Tuple< , >, … will only be used as utilities in the category theory via C# posts, instead of as functor or bifunctor. Here is a scenario for Tuple< , >, so its lazy version Lazy< , > can be created:
public class Lazy<T1, T2> { private readonly Lazy<Tuple<T1, T2>> lazy; public Lazy(Func<T1> factory1, Func<T2> factory2) : this(() => Tuple.Create(factory1(), factory2())) { } public Lazy(T1 value1, T2 value2) : this(() => Tuple.Create(value1, value2)) { } public Lazy(Func<Tuple<T1, T2>> factory) { this.lazy = new Lazy<Tuple<T1, T2>>(factory); } public T1 Value1 { [Pure]get { return this.lazy.Value.Item1; } } public T2 Value2 { [Pure]get { return this.lazy.Value.Item2; } } }
The difference from Lazy<> functor is, as the definition said, Lazy< , > wraps 2 types of values.
To make Lazy< , > a bifunctor, just create these bi-Select extension methods (in Haskell this is called bimap):
// [Pure] public static partial class LazyExtensions { public static Lazy<TResult1, TResult2> Select<TSource1, TSource2, TResult1, TResult2> (this Lazy<TSource1, TSource2> source, Func<TSource1, TResult1> selector1, Func<TSource2, TResult2> selector2) => new Lazy<TResult1, TResult2>(() => selector1(source.Value1), () => selector2(source.Value2)); public static IMorphism<Lazy<TSource1, TSource2>, Lazy<TResult1, TResult2>, DotNet> Select<TSource1, TSource2, TResult1, TResult2> (IMorphism<TSource1, TResult1, DotNet> selector1, IMorphism<TSource2, TResult2, DotNet> selector2) => new DotNetMorphism<Lazy<TSource1, TSource2>, Lazy<TResult1, TResult2>>( source => source.Select(selector1.Invoke, selector2.Invoke)); }
The difference from Lazy<> functor is - there are 2 selectors, one selector for each wrapped type.
Unit tests
The following unit test demonstrates the usage and laziness of Lazy< , >:
[TestClass()] public class BinaryFunctorTests { [TestMethod()] public void LazyTest() { bool isExecuted1 = false; bool isExecuted2 = false; Lazy<int, string> lazyBinaryFunctor = new Lazy<int, string>(1, "abc"); Func<int, bool> selector1 = x => { isExecuted1= true; return x > 0; }; Func<string, int> selector2 = x => { isExecuted2 = true; return x.Length; }; Lazy<bool, int> query = lazyBinaryFunctor.Select(selector1, selector2); Assert.IsFalse(isExecuted1); // Laziness. Assert.IsFalse(isExecuted2); // Laziness. Assert.AreEqual(true, query.Value1); // Execution. Assert.AreEqual("abc".Length, query.Value2); // Execution. Assert.IsTrue(isExecuted1); Assert.IsTrue(isExecuted2); } }
Please notice Tuple< , > does not have such laziness.
![image_thumb[2] image_thumb[2]](https://aspblogs.z22.web.core.windows.net/dixin/Windows-Live-Writer/Category-Theory-via-C-9-Functor-Category_8A55/image_thumb2_thumb.png)